练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a，b不共线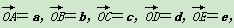，，设t∈R，如果3a＝c,2b＝d，e＝t(a＋b)，是否存在实数t使C，D，E三点在一条直线上？若存在，求出实数t的值；若不存在，请说明理由．


    解　由题设知，＝e－c＝(t－3)a＋tb，C，D，E三点在一条直线上的充要条件是存在实数k，使得，即(t－3)a＋tb＝－3ka＋2kb.

    整理得(t－3＋3k)a＝(2k－t)b.

    因为a，b不共线，所以有解得t＝.

    故存在实数t＝使C，D，E三点在一条直线上．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    下列函数中周期为π且为偶函数的是(　　)

    A．y＝sin                       B．y＝cos

    C．y＝sin                         D．y＝cos

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在锐角△ABC中，若BC＝2，sinA＝，则的最大值为(　　)

    A.                                    B.

    C．1                                    D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若△ABC的内角满足sinA＋sinB＝2sinC，则cosC的最小值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角梯形ABCD中，∠A＝90°，∠B＝30°，AB＝2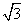，BC＝2，点E在线段CD上，若，则μ的取值范围是(　　)

    A．[0,1]                                B．[0，]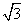

    C.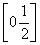                                D.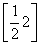

    查看答案和解析>>

    科目：高中数学 来源： 题型：


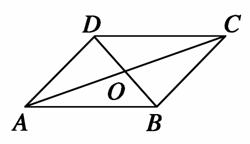
    如图，设O是平行四边形ABCD的两条对角线AC，BD的交点，下列向量组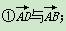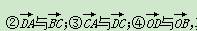：其中可作为这个平行四边形所在平面的一组基底的是(　　)

    A．①②                                 B．③④

    C．①③                                 D．①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知A(－3,0)，B(0，)，O为坐标原点，C在第二象限，且∠AOC＝30°，＝λ＋，则实数λ的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，平面四边形ABCD中，AB＝13，AC＝10，AD＝5，cos∠DAC＝，＝120.

    (1)求cos∠BAD；

    (2)设求x，y的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


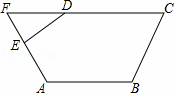
    如图，五边形ABCDE中，∠A=135°，延长CD，AE交于点F，且∠DEF=105°，∠F=45°，∠C=60°．

    （1）求∠B的度数；

    （2）AB与CD之间是否存在某种关系，说出你的理由．

     

    查看答案和解析>>

    同步练习册答案