【答案】
分析:(1)求出函数f(x)=x
2+ax+3-a图象的对称轴为x=-
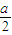
.由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围.
(2)当a≥0时,m(a)=f(0)=3-a;当-4≤a<0时,m(a)=f(-

)=-

a
2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及其相应的a值.
(3)公共点的横坐标x满足x
2+ax+3-a=|x
2-2x-3|.即x是方程a(x-1)=|x
2-2x-3|-x
2-3的实数解.设h(x)=|x
2-2x-3|-x
2-3,由此入手进行研究,能够得到结论.
解答:解:(1)函数f(x)=x
2+ax+3-a图象的对称轴为x=-
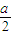
.
因为f(x)在闭区间[-1,3]上是单调函数,所以-

≤-1或-

≥3.
故a≤-6,或a≥2.…(4分)
(2)当a≥0时,m(a)=f(0)=3-a;
当-4≤a<0时,m(a)=f(-

)=-

a
2-a+3;
当a<-4时,m(a)=f(2)=a+7.…(2分)
所以,m(a)=

,
分段讨论并比较大小得,当a=-2时,m(a)有最大值4.…(6分)
(3)公共点的横坐标x满足x
2+ax+3-a=|x
2-2x-3|.
即x是方程a(x-1)=|x
2-2x-3|-x
2-3的实数解.
设h(x)=|x
2-2x-3|-x
2-3,
则直线y=a(x-1)与y=h(x)有公共点时的横坐标与上述问题等价.
当x≤-1或x≥3时,h(x)=|x
2-2x-3|-x
2-3=-2x-6;
解方程-2x-6=a(x-1),即(a+2)x=a-6,得x=

,a≠-2;…(1分)
当-1≤x≤3时,h(x)=|x
2-2x-3|-x
2-3=-2x
2+2x.
解方程-2x
2+2x=a(x-1),
即2x
2+(a-2)x-a=0,得
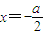
或x=1;…(2分)
研究结论及评分示例:(满分6分)
结论1:无论a取何实数值,点(1,4)必为两函数图象的公共点.…(1分)
结论2:(对某些具体的a取值进行研究).…(2分)
当a=-2时,两图象有一个公共点(1,4);
当a=-6时,公共点有2个,坐标为(1,4),(3,0);
当a=2时,公共点有2个,坐标为(1,4)、(-1,0).
(对每一个具体的a取值,结论正确给(1分),总分值不超过2分)
结论3:当-2<a<2,-6<a<-2时,公共点有3个,
坐标为(1,4)、(-

,|
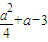
|)、(
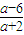
,
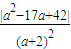
).…(4分)
点评:本题考查二次函数的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

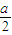 .由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围.
.由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围. )=-
)=- a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及其相应的a值.
a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及其相应的a值.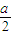 .
. ≤-1或-
≤-1或- ≥3.
≥3. )=-
)=- a2-a+3;
a2-a+3; ,
, ,a≠-2;…(1分)
,a≠-2;…(1分)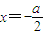 或x=1;…(2分)
或x=1;…(2分) ,|
,|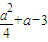 |)、(
|)、(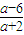 ,
,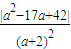 ).…(4分)
).…(4分)

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<