
分析 根据题意,由抛物线的方程可得其焦点坐标,作出图形分析可得|AG|=|FG|,用p表示|AG|、|FG|,可得|3+2$\sqrt{2}$-$\frac{p}{2}$|=$\sqrt{2p(3+2\sqrt{2})}$,解可得p的值,即可得答案.
解答 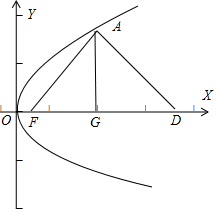 解:根据题意,如图,过点A作AG⊥x轴,
解:根据题意,如图,过点A作AG⊥x轴,
抛物线C:y2=2px,其焦点坐标为($\frac{p}{2}$,0),
又由△ADF为等腰直角三角形,且|FA|=|AD|,
则有|AG|=|FG|,
又由点A的横坐标为3+2$\sqrt{2}$,设其纵坐标为yb,
则|FG|=|3+2$\sqrt{2}$-$\frac{p}{2}$|,
点A的横坐标为3+2$\sqrt{2}$,yb2=2p(3+2$\sqrt{2}$),
则有|3+2$\sqrt{2}$-$\frac{p}{2}$|=$\sqrt{2p(3+2\sqrt{2})}$,
解可得p=2或34+24$\sqrt{2}$,
故抛物线的方程为y2=4x,
故答案为:y2=4x或y2=(68+48$\sqrt{2}$)x.
点评 本题考查抛物线的几何性质,关键是利用等腰直角三角形的性质分析.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1和侧面CDD1C1都是矩形,BC∥AD,△ABD是边长为2的正三角形,E,F分别为AD,A1D1的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1和侧面CDD1C1都是矩形,BC∥AD,△ABD是边长为2的正三角形,E,F分别为AD,A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
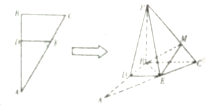 如图,在△ABC中,AB⊥BC,点D,E分别在AB,AC上,AD=2DB,AC=3EC,沿DE将△ADE翻折起来,使得点A到P的位置,满足$PB=\sqrt{3}BD$.
如图,在△ABC中,AB⊥BC,点D,E分别在AB,AC上,AD=2DB,AC=3EC,沿DE将△ADE翻折起来,使得点A到P的位置,满足$PB=\sqrt{3}BD$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com