
 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1和侧面CDD1C1都是矩形,BC∥AD,△ABD是边长为2的正三角形,E,F分别为AD,A1D1的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1和侧面CDD1C1都是矩形,BC∥AD,△ABD是边长为2的正三角形,E,F分别为AD,A1D1的中点.分析 (Ⅰ)证明DD1⊥AD,且DD1⊥CD,即可证明:DD1⊥平面ABCD;
(Ⅱ)证明BE⊥平面ADD1A1.即可证明:平面A1BE⊥平面ADD1A1;
(Ⅲ)证明四边形BCFA1是平行四边形,求棱BC的长度.
解答 (Ⅰ)证明:因为侧面ADD1A1和侧面CDD1C1都是矩形,
所以DD1⊥AD,且DD1⊥CD.
因为AD∩CD=D,
所以DD1⊥平面ABCD.…(4分)
(Ⅱ)证明:因为△ABD是正三角形,且E为AD中点,
所以BE⊥AD.
因为DD1⊥平面ABCD,
而BE?平面ABCD,
所以BE⊥DD1.
因为AD∩DD1=D,
所以BE⊥平面ADD1A1.
因为BE?平面A1BE,
所以平面A1BE⊥平面ADD1A1.…(10分)
(Ⅲ)解:因为BC∥AD,F为A1D1的中点,
所以BC∥A1F.
所以B、C、F、A1四点共面.
因为CF∥平面A1BE,
而平面BCFA1∩平面A1BE=A1B,
所以CF∥A1B.
所以四边形BCFA1是平行四边形.
所以$BC=F{A_1}=\frac{1}{2}AD=1$.…(14分)
点评 本题考查线面垂直、面面垂直,考查线面平行的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
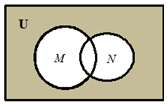 已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )
已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )| A. | {x|x<2} | B. | {x|1<x<2} | C. | {x|x>3} | D. | {x|x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
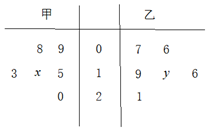 如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.
如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com