
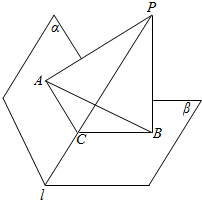
分析 点P可能在二面角α-l-β内部,也可能在外部,应区别处理.过P点向平面α平面β和直线l做垂线,垂足分别为A,B,C,连接AC,BC,我们可得∠ACB锐二面角α-l-β的平面角,由此能求出二面角的大小.
解答 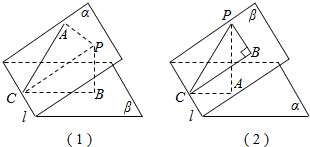 解:点P可能在二面角α-l-β内部,也可能在外部,应区别处理.∵PA⊥α,交α于A,AC⊥l,交l于C,连结PC,
解:点P可能在二面角α-l-β内部,也可能在外部,应区别处理.∵PA⊥α,交α于A,AC⊥l,交l于C,连结PC,
∴由三垂线定理得PC⊥l,
∵PB⊥β,交β于B,连结BC,
∴由PC⊥l,利用三垂线定理的逆定理得BC⊥l,
∴∠ACB是二面角α-l-β的平面角,
∵CA、CP、CB同时垂直于l,
∴A、C、B、P四点共面,∠PAC=∠PBC=90°,
∵由题设条件,得PA=4,PB=3,PC=$\frac{2\sqrt{39}}{3}$,
∴AC=$\sqrt{(\frac{2\sqrt{39}}{3})^{2}-16}$=$\frac{2\sqrt{3}}{3}$,BC=$\sqrt{(\frac{2\sqrt{39}}{3})^{2}-9}=\frac{5\sqrt{3}}{3}$,
∴tan∠ACP=$\frac{AP}{AC}$=2$\sqrt{3}$,tang$∠PCB=\frac{BP}{BC}$=$\frac{3\sqrt{3}}{5}$,
当点P在二面角α-l-β的内部时,如图(1),
∠ACB=∠ACP+∠PCB,
∴tan∠ACB=tan(∠ACP+∠PCB)=$\frac{tan∠ACP+tan∠PCB}{1-tan∠ACPtan∠PCB}$=$\frac{2\sqrt{3}+\frac{3\sqrt{3}}{5}}{1-2\sqrt{3}×\frac{3\sqrt{3}}{5}}$=-$\sqrt{3}$,
∴∠ACB=$\frac{2π}{3}$.
当点P在二面角α-l-β的外部时,如图(2),
∠ACB=∠PCB-∠ACP,
∴tan∠ACB=tan(∠ACP-∠PCB)=$\frac{tan∠ACP-tan∠PCB}{1+tan∠ACPtan∠PCB}$=$\frac{2\sqrt{3}-\frac{3\sqrt{3}}{5}}{1+2\sqrt{3}×\frac{3\sqrt{3}}{5}}$=$\frac{7\sqrt{3}}{23}$,
∴∠ACB=arctan$\frac{7\sqrt{3}}{23}$.
∴二面角α-l-β的大小为$\frac{2π}{3}$或arctan$\frac{7\sqrt{3}}{23}$.
点评 本题考查的知识点是二面角的平面角及求法,其中根据二面角的定义,结合已知条件构造出∠ACB锐二面角α-l-β的平面角,是解答本题的关键.


科目:高中数学 来源: 题型:解答题
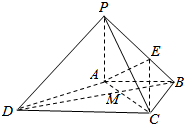 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
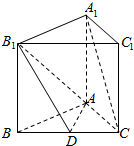 已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.
已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
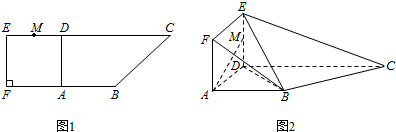
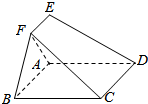 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com