已知数列{an}的前n项和为Sn，若a1=-2，a2=2，且an+2-an=1+（-1）n，则S50=________．
600
分析：通过对n的讨论是奇数函数偶数，判断出数列的奇数项是常数列，偶数项是等差数列，利用分组的方法将数列{a
n}分成两个数列，再利用等差数列的前n项和公式求出和．
解答：∵a
n+2-a
n=1+（-1）
n
∴当n为偶数时，a
n+2-a
n=2；当n为奇数时，a
n+2-a
n=0
∴a
1，a
3，a
5…为常数列-2；a
2，a
4，a
6…为以2为首项，以2为公差的等差数列
∴S
50=（（a
1+a
3+a
5…+a
49）+（a
2+a
4+a
6+…+a
50）
=25×（-2）
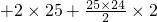
=600
故答案为600．
点评：求数列的前n项和，首项根据数列的通项特点．选择合适的求和方法，故关键是求出数列的通项．
