
【题目】自2016年底,共享单车日渐火爆起来,逐渐融入大家的日常生活中,某市针对18岁到80岁之间的不同年龄段的城市市民使用共享单车情况进行了抽样调查,结果如下表所示:

(1)采用分层抽样的方式从年龄在![]() 内的人中抽取
内的人中抽取![]() 人,求其中男性、女性的使用人数各为多少?
人,求其中男性、女性的使用人数各为多少?
(2)在(1)中选出![]() 人中随机抽取4人,求其中恰有2人是女性的概率;
人中随机抽取4人,求其中恰有2人是女性的概率;
(3)用样本估计总体,在全市18岁到80岁的市民中抽4人其中男性使用的人数记为![]() ,求
,求![]() 的分布列。
的分布列。
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() =1(a>0,b>0)的离心率与双曲线
=1(a>0,b>0)的离心率与双曲线![]() =1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin
=1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin![]() ·x+cos
·x+cos![]() ·y-l=0相切(
·y-l=0相切(![]() 为常数).
为常数).
(1)求椭圆C的方程;
(2)若过点M(3,0)的直线与椭圆C相交TA,B两点,设P为椭圆上一点,且满足![]() (O为坐标原点),当
(O为坐标原点),当![]() 时,求实数t取值范围.
时,求实数t取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]()
![]() (
(![]() )的半焦距为
)的半焦距为![]() ,原点
,原点![]() 到经过两点
到经过两点![]() ,
,![]() 的直线的距离为
的直线的距离为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)如图,![]() 是圆
是圆![]()
![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国海军,正在以不可阻挡的气魄向深蓝进军.在中国海军加快建设的大背景下,国产水面舰艇吨位不断增大、技术日益现代化,特别是国产航空母舰下水,航母需要大量高素质航母舰载机飞行员.为此中国海军在全国9省9所优质普通高中进行海航班建设试点培育航母舰载机飞行员.2017年4月我省首届海军航空实验班开始面向全省遴选学员,有10000名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收50名学员.培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”),这批海航班学员在10月参加活动的次数统计如图所示:
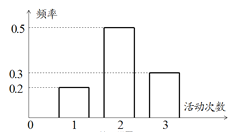
(1)从海航班学员中任选2名学员,求他们10月参加活动次数恰好相等的概率;
(2)从海航班学员中任选2名学员,用![]() 表示这两学员10月参加活动次数之差绝对值,求随机变量
表示这两学员10月参加活动次数之差绝对值,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市甲、乙两地为了争创“市级文明城市”,现市文明委对甲、乙两地各派10名专家进行打分评优,所得分数情况如下茎叶图所示.
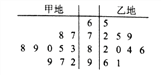
(1)分别计算甲、乙两地所得分数的平均值,并计算乙地得分的中位数;
(2)从乙地所得分数在![]() 间的成绩中随机抽取2份做进一步分析,求所抽取的成绩中,至少有一份分数在
间的成绩中随机抽取2份做进一步分析,求所抽取的成绩中,至少有一份分数在![]() 间的概率;
间的概率;
(3)在甲、乙两地所得分数超过90分的成绩中抽取其中2份分析其合理性,求这2份成绩都是来自甲地的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 360,则判断框中可以填( )
的值为 360,则判断框中可以填( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥 P - ABCD 中,锐角三角形 PAD 所在平面垂直于平面 PAB,AB⊥AD,AB⊥BC。

(1) 求证:BC∥平面 PAD;
(2) 平面 PAD⊥ 平面 ABCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com