
【题目】
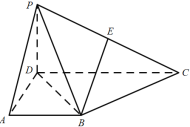
在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 中点,底面
中点,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() =90°,
=90°,![]() ,
,![]() .
.
(I)求证:![]()
![]() 平面
平面![]() ;
;
(II)求证:![]() 平面
平面![]() ;
;
(III)设![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 为45°.
为45°.
【答案】(I)证明见解析.
(II)证明见解析.
(III)![]()
【解析】
(I)取PD的中点F,连结EF,AF,
因为E为PC中点,所以EF//CD,且![]()
在梯形ABCD中,AB//CD,AB=1,
所以EF//AB,EF=AB,四边形ABEF为平行四边形,
所以BE//AF,
BE![]() 平面PAD,AF
平面PAD,AF![]() 平面PAD,
平面PAD,
所以BE//平面PAD.
(II)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,
所以PD⊥AD.
如图,以D为原点建立空间直角坐标系D—xyz.
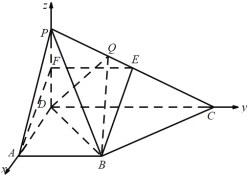
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1).
![]()
所以![]()
![]()
又由PD⊥平面ABCD,可得PD⊥BC,
所以BC⊥平面PBD.
(III)平面PBD的法向量为
![]()
![]()
所以![]() ,
,
设平面QBD的法向量为![]() =(a,b,c),
=(a,b,c),
![]() ,
,
由![]()
![]() ,
,![]()
![]() ,得
,得 ![]()
所以![]() =
=![]()
所以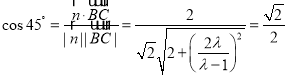
注意到![]() ,得
,得![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆C:![]() 的左、右焦点,椭圆C过点M
的左、右焦点,椭圆C过点M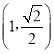 ,且MF2⊥F1F2.
,且MF2⊥F1F2.
(1)求椭圆C的方程;
(2)经过点P(2,0)的直线交椭圆C于A,B两点,若存在点Q(m,0),使得|QA|=|QB|.
①求实数m的取值范围:
②若线段F1A的垂直平分线过点Q,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校李老师本学期任高一A班、B班两个班数学课教学,两个班都是50个学生,下图反映的是两个班在本学期5次数学检测中的班级平均分对比,根据图表信息,下列不正确的结论是( )

A. A班的数学成绩平均水平好于B班
B. B班的数学成绩没有A班稳定
C. 下次B班的数学平均分高于A班
D. 在第一次考试中,A、B两个班总平均分为78分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
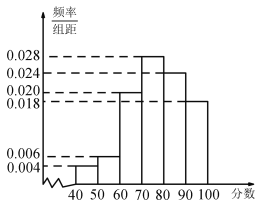
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年11月26日,联合国教科文组织宣布3月14日为“国际数学日”(昵称:![]() ),2020年3月14日是第一个“国际数学日”.圆周率
),2020年3月14日是第一个“国际数学日”.圆周率![]() 是圆的周长与直径的比值,是一个在数学及物理学中普遍存在的数学常数.
是圆的周长与直径的比值,是一个在数学及物理学中普遍存在的数学常数.![]() 有许多奇妙性质,如莱布尼兹恒等式
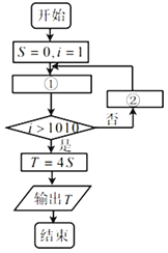
有许多奇妙性质,如莱布尼兹恒等式![]() ,即为正奇数倒数正负交错相加等.小红设计了如图所示的程序框图,要求输出的
,即为正奇数倒数正负交错相加等.小红设计了如图所示的程序框图,要求输出的![]() 值与
值与![]() 非常近似,则①、②中分别填入的可以是( )
非常近似,则①、②中分别填入的可以是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥![]() 的底面正方形边长是3,
的底面正方形边长是3,![]() 是在底面上的射影,
是在底面上的射影,![]() ,
,![]() 是
是![]() 上的一点,过
上的一点,过![]() 且与
且与![]() 、
、![]() 都平行的截面为五边形
都平行的截面为五边形![]() .
.
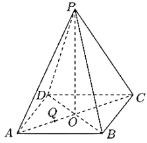
(1)在图中作出截面![]() ,并写出作图过程;
,并写出作图过程;
(2)求该截面面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com