
【题目】如果一个三位数abc同时满足![]() 且
且![]() ,则称该三位数为“凹数”,那么所有不同的三位“凹数”的个数是______.
,则称该三位数为“凹数”,那么所有不同的三位“凹数”的个数是______.
【答案】285
【解析】
根据题意可得十位比百位小,并且十位比个位小,因此首先对十位依次进行分类讨论,分别求出每种情况的“凹数”的个数,由加法原理计算可得答案.
根据题意,按十位数字分类讨论:
![]() 十位数字是9时不存在,此时三位“凹数”的个数为0;
十位数字是9时不存在,此时三位“凹数”的个数为0;
![]() 十位数字是8,只有989,此时三位“凹数”的个数为1;
十位数字是8,只有989,此时三位“凹数”的个数为1;
![]() 十位数字是7,则百位与个位都有2种可能,所以此时三位“凹数”的个数为
十位数字是7,则百位与个位都有2种可能,所以此时三位“凹数”的个数为![]() ;
;
![]() 十位数字是6,则百位与个位都有3种可能,所以此时三位“凹数”的个数为
十位数字是6,则百位与个位都有3种可能,所以此时三位“凹数”的个数为![]() ;
;
![]() 十位数字是5,则百位与个位都有4种可能,所以此时三位“凹数”的个数为
十位数字是5,则百位与个位都有4种可能,所以此时三位“凹数”的个数为![]() ;
;
![]() 十位数字是4时,则百位与个位都有5种可能,所以此时三位“凹数”的个数为
十位数字是4时,则百位与个位都有5种可能,所以此时三位“凹数”的个数为![]() ;
;
![]() 十位数字是3时,则百位与个位都有6种可能,所以此时三位“凹数”的个数为
十位数字是3时,则百位与个位都有6种可能,所以此时三位“凹数”的个数为![]() ;
;
![]() 十位数字是2时,则百位与个位都有7种可能,所以此时三位“凹数”的个数为
十位数字是2时,则百位与个位都有7种可能,所以此时三位“凹数”的个数为![]() ;
;
![]() 十位数字是1时,则百位与个位都有8种可能,所以此时三位“凹数”的个数为
十位数字是1时,则百位与个位都有8种可能,所以此时三位“凹数”的个数为![]() ;
;
![]() 十位数字是0时,则百位与个位都有9种可能,所以此时三位“凹数”的个数为
十位数字是0时,则百位与个位都有9种可能,所以此时三位“凹数”的个数为![]() ,
,
所以所有不同的三位“凹数”的个数是![]() 个,
个,
故答案为:285.


科目:高中数学 来源: 题型:
【题目】某校在高二数学竞赛初赛后,对90分及以上的成绩进行统计,其频率分布直方图如图所示,若![]() 分数段的参赛学生人数为2.
分数段的参赛学生人数为2.
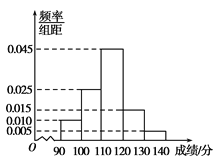
(1)求该校成绩在![]() 分数段的参赛学生人数;
分数段的参赛学生人数;
(2)估计90分及以上的学生成绩的众数、中位数和平均数(结果保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有三家工厂,分别位于矩形ABCD的顶点A,B以及CD的中点P处,已知AB=20km,CB=10km,为了处理三家工厂的污水,现要在矩形ABCD内(含边界),且与A,B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为![]() km.
km.

(I)设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
(II)确定污水处理厂的位置,使三条排污管道的总长度最短,并求出最短值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一年级某个班分成7个小组,利用假期参加社会公益服务活动![]() 每个小组必须全员参加
每个小组必须全员参加![]() ,参加活动的次数记录如下:
,参加活动的次数记录如下:
组别 |
|
|
|
|
|
|
|
参加活动次数 | 3 | 2 | 4 | 3 | 3 | 4 | 2 |
![]() Ⅰ
Ⅰ![]() 求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
![]() Ⅱ
Ⅱ![]() 从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
![]() Ⅲ
Ⅲ![]() 至
至![]() 小组每组有4名同学,
小组每组有4名同学,![]() 小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为
小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为![]() ,写出
,写出![]() 与v的大小关系
与v的大小关系![]() 结论不要求证明
结论不要求证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:
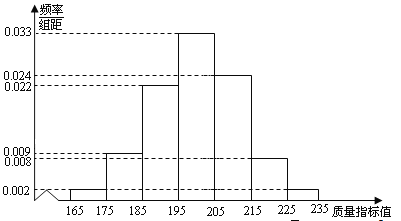
(I)求这500件产品质量指标值的样本平均值![]() 和样本方差
和样本方差![]() (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)某用户从该企业购买了100件这种产品,记![]() 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间![]() 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求![]() .
.
附:![]()
若![]() 则
则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的两个三等分点.若把等腰梯形沿虚线
的两个三等分点.若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() ,如图(2).
,如图(2).

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com