Question

1．若函数f（x）在定义域D内的某个区间I上是增函数，且F（x）=$\frac{f（x）}{x}$在I上也是增函数，则称y=f（x）是I上的“完美增函数”．已知f（x）=e^x+x，g（x）=e^x+x-lnx+1．
（1）判断函数f（x）是否为区间（0，+∞）上的“完美增函数”；
（2）若函数g（x）是区间$[{\frac{m}{2}，+∞}）$上的“完美增函数”，求整数m的最小值．

Answer 1

分析 （1）证明f（x）在区间（0，+∞）上是增函数，F（x））在区间（0，+∞）上不一定是增函数，即可得出函数f（x）是否为区间（0，+∞）上的“完美增函数”；
（2）g（x）=e^x+x-lnx+1，与G（x）=$\frac{g（x）}{x}$在[$\frac{3}{2}$，+∞）上都是单调递增函数，即可求整数m的最小值．

解答 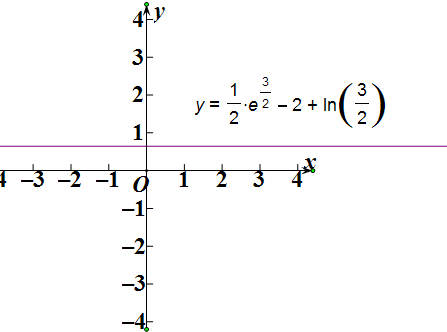解：（1）∵f（x）=e^x+x，∴f′（x）=e^x+1＞0，
∴f（x）在区间（0，+∞）上是增函数，
∵F（x）=$\frac{f（x）}{x}$=$\frac{{e}^{x}}{x}$+1，
∴F′（x）=$\frac{{e}^{x}（x-1）}{{x}^{2}}$≥0）在区间（0，+∞）上不恒成立，
∴F（x））在区间（0，+∞）上不一定是增函数，
∴函数f（x）不是区间（0，+∞）上的“完美增函数”；
（2）∵g（x）=e^x+x-lnx+1，x＞0，
∴g′（x）=e^x+1-$\frac{1}{x}$在（0，+∞）单调递增，g′（$\frac{1}{2}$）=$\sqrt{e}$-1＞0，
∴可以得出：g（x）在[$\frac{1}{2}$，+∞）上是单调递增．
∵G（x）=$\frac{{e}^{x}+x-lnx+1}{x}$，
∴G′（x）=$\frac{{e}^{x}（x-1）+lnx-2}{{x}^{2}}$，x＞0，
设m（x）=xe^x-e^x-2+lnx，
m′（x）=xe^x+$\frac{1}{x}$＞0，m（x）在（0，+∞）上单调递增，
m（$\frac{1}{2}$）=-$\frac{1}{2}$${e}^{\frac{1}{2}}$-2-ln2＜0，m（1）=e-e-2+0=-2＜0，
m（$\frac{3}{2}$）=$\frac{1}{2}{e}^{\frac{3}{2}}$-2+ln（$\frac{3}{2}$）＞0（根据图象判断）
∴在[$\frac{3}{2}$，+∞）上，有G′（x）＞0成立，
∴函数G（x）=$\frac{g（x）}{x}$在[$\frac{3}{2}$，+∞）上是单调递增函数，
综合判断：g（x）=e^x+x-lnx+1，与G（x）=$\frac{g（x）}{x}$在[$\frac{3}{2}$，+∞）上都是单调递增函数，
g（x）=e^x+x-lnx+1，与G（x）=$\frac{g（x）}{x}$在[1，+∞）上不是都为单调递增函数，
∵函数g（x）是区间$[{\frac{m}{2}，+∞}）$上的“完美函数”，
∴m≥3，
即整数m最小值为3．

点评 本题以新定义的形式考查函数的单调性，考查运用所学知识分析解决新问题的能力，多次构造函数，求解导数，判断的递增，思路要清晰，属于难题．