
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
分析 由函数f(x)=-$\frac{1}{3}{x}^{3}+\frac{a}{2}{x}^{2}+bx$有两个极值点x1,x2,可得x2-ax-b=0有两个不相等的根,必有△=a2+4b>0.而方程f2(x)-af(x)-b=0的△1=△>0,可知此方程有两解且f(x)=x1或x2.再分别讨论利用平移变换即可解出方程f(x)=x1或f(x)=x2解的个数.
解答 解:∵f(x)=-$\frac{1}{3}{x}^{3}+\frac{a}{2}{x}^{2}+bx$,
∴f′(x)=-x2+ax+b,
由题意知x1,x2是函数的两个极值点,
∴x2-ax-b=0有两个不相等的根,
∴△=a2+4b>0.
∵x1<x2,
∴x1=$\frac{a-\sqrt{{a}^{2}+4b}}{2}$,x2=$\frac{a+\sqrt{{a}^{2}+4b}}{2}$.
而方程f2(x)-af(x)-b=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2
即有0<x1<x2,f(x2)>0.
①把y=f(x)向下平移x2个单位即可得到y=f(x)-x2的图象,
∵f(x2)=x2,可知方程f(x)=x2有两解.
②把y=f(x)向下平移x1个单位即可得到y=f(x)-x1的图象,
∵f(x2)=x2,∴f(x2)-x1>0,可知方程f(x)=x1只有一解.
综上①②可知:方程f(x)=x1或f(x)=x2只有3个实数解.
即关于x的方程f2(x)-af(x)-b=0的只有3不同实根.
故选:B.
点评 本题综合考查了利用导数研究函数得单调性、极值及方程解得个数、平移变换等基础知识,考查了图象平移的思想方法、推理能力、计算能力、分析问题和解决问题的能力.


科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(文)试卷(解析版) 题型:选择题
将函数 的图象向左平移
的图象向左平移 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间 上单调递减 B.在区间
上单调递减 B.在区间 上单调递增
上单调递增
C.在区间 上单调递减 D.在区间
上单调递减 D.在区间 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)为偶函数 | B. | f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上单调递增 | ||
| C. | x=$\frac{π}{2}$为f(x)的图象的一条对称轴 | D. | ($\frac{π}{2}$,0)为f(x)的图象的一个对称中心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y≥-1 | B. | x≥2 | C. | x+2y+2≥0 | D. | 2x-y+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
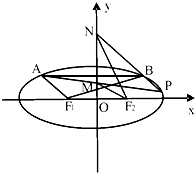 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com