
| A. | f(x)为偶函数 | B. | f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上单调递增 | ||
| C. | x=$\frac{π}{2}$为f(x)的图象的一条对称轴 | D. | ($\frac{π}{2}$,0)为f(x)的图象的一个对称中心 |
分析 利用两角和差的正弦公式将函数f(x)进行化简,利用函数的周期求出ω即可得到结论.
解答 解:f(x)=sin(ωx+$\frac{π}{3}$)+$\sqrt{3}$sin(ωx-$\frac{π}{6}$)=f(x)=sin(ωx+$\frac{π}{3}$)+$\sqrt{3}$sin(ωx+$\frac{π}{3}$-$\frac{π}{2}$)
=sin(ωx+$\frac{π}{3}$)-$\sqrt{3}$cosωx+$\frac{π}{3}$)
=2sin(ωx+$\frac{π}{3}$-$\frac{π}{3}$)=2sinωx.
∵f(x)的最小正周期为π,
∴T=$\frac{2π}{ω}=π$,解得ω=2,
即f(x)=2sin2x.
∵f($\frac{π}{2}$)=2sin(2×$\frac{π}{2}$)=2sinπ=0,
∴($\frac{π}{2}$,0)为f(x)的图象的一个对称中心.
故选:D
点评 本题主要考查三角函数的图象和性质,利用两角和差的正弦公式求出ω是解决本题的关键.


科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(文)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图,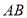 是
是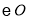 的直径,
的直径,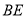 为
为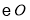 的切线,点
的切线,点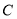 为
为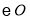 上不同于
上不同于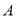 、
、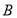 的一点,
的一点,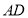 为
为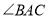 的平分线,且分别与
的平分线,且分别与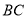 交于
交于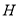 ,与
,与 交于
交于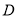 ,与
,与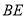 交于
交于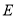 ,连接
,连接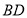 、
、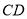 .
.
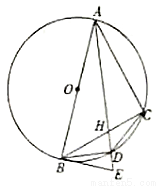
(Ⅰ)求证: ;
;
(Ⅱ)求证: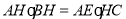 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )| A. | $\frac{10}{3}$ | B. | 3 | C. | $\frac{14}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2] | C. | $[{\frac{{\sqrt{3}-3}}{4},\frac{{\sqrt{3}+3}}{4}}]$ | D. | $[{0,\frac{12}{5}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
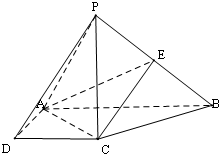 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com