
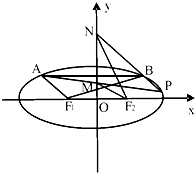
 ��ͼ��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬�ҽ���Ϊ2$\sqrt{2}$������ABƽ����x�ᣬ��|F1A|+|F2A|=4��
��ͼ��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬�ҽ���Ϊ2$\sqrt{2}$������ABƽ����x�ᣬ��|F1A|+|F2A|=4������ ��������֪���$c=\sqrt{2}$��a=2��������������õ�b2=a2-c2=2������Բ���̿���
������B��x0��y0����P��x1��y1������A��-x0��y0������ֱ�߷��̵�б��ʽ���ֱ��AP�ķ��̣�ȡx=0�����yֵ�����ɵõ�M���꣬ͬ���ɵ�N�����꣮��������б�ʵõ�k1��k2��������A��B����ԲC�ϣ��õ�k1•k2=1����$|{k}_{1}+{k}_{2}|=|{k}_{1}|+|{k}_{2}|��2\sqrt{|{k}_{1}||{k}_{2}|}=2$������k1=k2ʱM��N�غϣ���A��B�غ���������������k1��k2�����ȺŲ��������Ӷ����k1+k2��ȡֵ��Χ��
��� �⣺���߽���Ϊ$2\sqrt{2}$����$2c=2\sqrt{2}$��$c=\sqrt{2}$��
��|F1A|+|F2A|=4����2a=4����a=2��
��b2=a2-c2=2��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$��
������B��x0��y0����P��x1��y1������A��-x0��y0����
ֱ��AP�ķ���Ϊ$y-{y}_{1}=\frac{{y}_{1}-{y}_{0}}{{x}_{1}+{x}_{0}}��x-{x}_{1}��$����x=0����$y=\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{{x}_{1}+{x}_{0}}$��
��$M��0��\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{{x}_{1}+{x}_{0}}��$��
ͬ���ɵ�$N��0��\frac{{x}_{1}{y}_{0}-{x}_{0}{y}_{1}}{{x}_{1}-{x}_{0}}��$��
��${k}_{1}=-\frac{{x}_{1}{y}_{0}+{x}_{0}{y}_{1}}{\sqrt{2}��{x}_{1}+{x}_{0}��}$��${k}_{2}=-\frac{{x}_{1}{y}_{0}-{x}_{0}{y}_{1}}{\sqrt{2}��{x}_{1}-{x}_{0}��}$
���${k}_{1}•{k}_{2}=\frac{1}{2}•\frac{{{x}_{1}}^{2}{{y}_{0}}^{2}-{{x}_{0}}^{2}{{y}_{1}}^{2}}{{{x}_{1}}^{2}-{{x}_{0}}^{2}}$��
��A��B����ԲC�ϣ���${{y}_{1}}^{2}=2-\frac{1}{2}{{x}_{1}}^{2}��{{y}_{0}}^{2}=2-\frac{1}{2}{{x}_{0}}^{2}$��
��${k}_{1}•{k}_{2}=\frac{1}{2}•\frac{{{x}_{1}}^{2}��2-\frac{1}{2}{{x}_{0}}^{2}��-{{x}_{0}}^{2}��2-\frac{1}{2}{{x}_{1}}^{2}��}{{{x}_{1}}^{2}-{{x}_{0}}^{2}}$=1
��$|{k}_{1}+{k}_{2}|=|{k}_{1}|+|{k}_{2}|��2\sqrt{|{k}_{1}||{k}_{2}|}=2$��
�֡ߵ�k1=k2ʱM��N�غϣ���A��B�غϣ�����������������k1��k2��
���k1+k2��ȡֵ��Χ�ǣ�-�ޣ�-2���ȣ�2��+�ޣ���
���� ���⿼������Բ���̵�������ֱ������Բλ�ù�ϵ��Ӧ�ã�ѵ���ˡ�������Ľ���˼�뷽����������ѧ��������������������ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
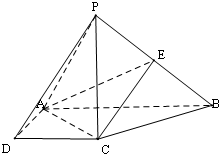 ��ͼ��������P-ABCD�У�PC�͵���ABCD������ABCD��ֱ�����Σ�AB��AD��AB��CD��AB=2AD=2CD=2��PC��2��E��PB���е㣮
��ͼ��������P-ABCD�У�PC�͵���ABCD������ABCD��ֱ�����Σ�AB��AD��AB��CD��AB=2AD=2CD=2��PC��2��E��PB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABC�У�PA=PB=2��PC=4����APB=��BPC=60�㣬cos��APC=$\frac{1}{4}$��
��ͼ��������P-ABC�У�PA=PB=2��PC=4����APB=��BPC=60�㣬cos��APC=$\frac{1}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����������һ����ѧ�����������ѧ������ѧ�Ծ��������棩 ���ͣ������
������ ��
�� ��������
�������� �ǵȱ����У���
�ǵȱ����У��� _____________��
_____________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com