
分析 由题意可得∠BAC 为钝角,再由$\frac{1}{2}$×2×3×sin∠BAC=$\frac{3}{2}$,解得sin∠BAC=$\frac{1}{2}$,从而得到∠BAC的值.
解答 解:∵在△ABC中,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,且△ABC的面积为$\frac{3}{2}$,
∴${S}_{△ABC}=\frac{1}{2}|\overrightarrow{AB}|•|\overrightarrow{AC}|•sin∠BAC$=$\frac{3}{2}$,
即$\frac{1}{2}×2×3×sin∠BAC=\frac{3}{2}$,解得sin∠BAC=$\frac{1}{2}$,
又$\overrightarrow{AB}$•$\overrightarrow{AC}$<0,∴$∠BAC∈(\frac{π}{2},π)$,
∴∠BAC=150°.
故答案为:150°.
点评 本题主要考查两个向量的数量积的定义及三角形的面积公式,考查已知三角函数值求角的大小,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
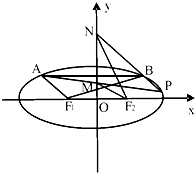 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:选择题
已知 是虚数单位,若复数
是虚数单位,若复数 在复平面内对应的点在第四象限,则实数
在复平面内对应的点在第四象限,则实数 的值可能是( )
的值可能是( )
A.-2 B.1
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com