
分析 (1)利用导数即可求出单调区间;
(2)分离参数,构造函数,求出函数的最小值即可;
(3)问题转化为$\frac{(a+x)ln(a+x)}{{e}^{a+x}}$<$\frac{alna}{{e}^{x}}$,构造函数g(x)=$\frac{xlnx}{{e}^{x}}$,则问题就是要求g(a+x)<g(a)恒成立,多次构造函数和求导,利用导数和函数最值的关系,得到存在最小的正常数m,问题得以解决.
解答 解:(1)∵f(x)=xlnx.
∴f′(x)=1+lnx,
当x∈(0,$\frac{1}{e}$)时,f′(x)<0;当x∈($\frac{1}{e}$,+∞)时,f′(x)>0.
所以函数f(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增.
(2)由于x>0,f(x)>kx-$\frac{1}{2}$恒成立,
∴k=lnx+$\frac{1}{2x}$.
构造函数k(x)=lnx+$\frac{1}{2x}$.
∴k′(x)=$\frac{1}{x}$-$\frac{1}{2{x}^{2}}$=$\frac{2x-1}{2{x}^{2}}$.
令k′(x)=0,解得x=$\frac{1}{2}$,
当x∈(0,$\frac{1}{2}$)时,k′(x)<0,当x∈($\frac{1}{2}$,+∞)时,k′(x)>0.
∴函数k(x)在点x=$\frac{1}{2}$处取得最小值,即k($\frac{1}{2}$)=1-ln2.
因此所求的k的取值范围是(-∞,1-ln2).
(3)结论:这样的最小正常数m存在.解释如下:
f(a+x)<f(a)•ex?(a+x)ln(a+x)<alna)•ex?$\frac{(a+x)ln(a+x)}{{e}^{a+x}}$<$\frac{alna}{{e}^{x}}$.
构造函数g(x)=$\frac{xlnx}{{e}^{x}}$,则问题就是要求g(a+x)<g(a)恒成立.
对于g(x)求导得 g′(x)=$\frac{lnx+1-xlnx}{{e}^{x}}$.
令h(x)=lnx+1-xlnx,则h′(x)=$\frac{1}{x}$-lnx-1,显然h′(x)是减函数.
又h′(1)=0,所以函数h(x)在(0,1)上是增函数,在(1,+∞)上是减函数,
而h($\frac{1}{{e}^{2}}$)=ln$\frac{1}{{e}^{2}}$+1-$\frac{1}{{e}^{2}}•ln\frac{1}{{e}^{2}}$=-2+1+$\frac{2}{{e}^{2}}$=$\frac{2-{e}^{2}}{{e}^{2}}$<0,
h(1)=ln1+1-ln1=1>0,h(e)=lne+1-elne=1+1-e=2-e<0.
所以函数h(x)在区间(0,1)和(1,+∞)上各有一个零点,令为x1和x2(x1<x2),
并且有:在区间(0,x1)和(x2,+∞)上,h(x)<0即g′(x)<0;
在区间(x1,x2)上,h(x)>0即g′(x)>0.
从而可知函数g(x)在区间(0,x1)和(x2,+∞)上单调递减,在区间(x1,x2)上单调递增.
g(1)=0,当0<x<1时,g(x)<0;当x>1时,g(x)>0.还有g(x2)是函数的极大值,也是最大值.
题目要找的m=x2,理由是:
当a>x2时,对于任意非零正数x,a+x>a+x2,而g(x)在(x2,+∞)上单调递减,
所以g(a+x)<g(a)一定恒成立,即题目所要求的不等式恒成立,
说明m≤x2;
当0<a<x2时,取x=x2-a,显然x>0且g(a+x)=g(x2)>g(a),
题目所要求的不等式不恒成立,说明m不能比x2小.
综合可知,题目所要寻求的最小正常数m就是x2,即存在最小正常数m=x2,当a>m时,对于任意正实数x,不等式不等式f(a+x)<f(a)•ex恒成立.
点评 本题主要考查了函数导数与单调性、零点以及不等式的问题,主要是利用导数研究函数的单调性等基础知识,考查计算能力和分析问题的能力,以及分类讨论思想,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2] | C. | $[{\frac{{\sqrt{3}-3}}{4},\frac{{\sqrt{3}+3}}{4}}]$ | D. | $[{0,\frac{12}{5}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
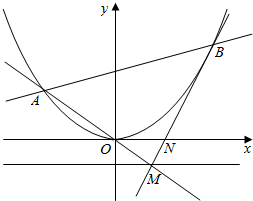 抛物线C:x2=4y,直线l1:y=kx交C于点A,交准线于点M.过点M的直线l2与抛物线C有唯一的公共点B(A,B在对称轴的两侧),且与x轴交于点N.
抛物线C:x2=4y,直线l1:y=kx交C于点A,交准线于点M.过点M的直线l2与抛物线C有唯一的公共点B(A,B在对称轴的两侧),且与x轴交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
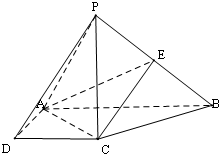 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com