
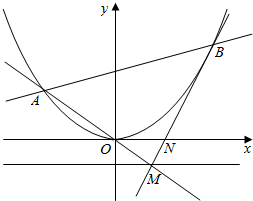
 抛物线C:x2=4y,直线l1:y=kx交C于点A,交准线于点M.过点M的直线l2与抛物线C有唯一的公共点B(A,B在对称轴的两侧),且与x轴交于点N.
抛物线C:x2=4y,直线l1:y=kx交C于点A,交准线于点M.过点M的直线l2与抛物线C有唯一的公共点B(A,B在对称轴的两侧),且与x轴交于点N.分析 (Ⅰ)根据抛物线的标准方程求出p的值,写出它的准线方程;
(Ⅱ)根据直线方程与抛物线的方程求出点A、B、M、N的坐标,表示出△MON与△AOB的面积,求出S△AOB:S△MON的取值范围.
解答  解:(Ⅰ)如图所示,
解:(Ⅰ)如图所示,
∵抛物线C:x2=4y,
∴p=2,
∴抛物线的准线方程为y=-1;…(4分)
(Ⅱ)不妨设点A在y轴的左侧,则M(-$\frac{1}{k}$,-1),
设l2的斜率为m,
∴它的直线方程为y+1=m(x+$\frac{1}{k}$),
与抛物线方程联立得$\left\{\begin{array}{l}{y+1=m(x+\frac{1}{k})}\\{{x}^{2}=4y}\end{array}\right.$,
消去y得,x2-4mx+4-$\frac{4m}{k}$=0,…(6分)
∴△=16m2-4(4-$\frac{4m}{k}$)=0,
解得$\frac{1}{k}$=$\frac{1{-m}^{2}}{m}$<0;…(8分)
∴B(2m,m2),且m>1;
A(4k,4k2),N($\frac{1}{m}$-$\frac{1}{k}$,0),ON=|$\frac{1}{m}$-$\frac{1}{k}$|=m,
∴△MON的面积为S△MON=$\frac{1}{2}$m;…(10分)
又点B到l1的距离为d=$\frac{|2km{-m}^{2}|}{\sqrt{{k}^{2}+1}}$,
OA=4|k|$\sqrt{1{+k}^{2}}$,
∴△AOB的面积为
S△AOB=$\frac{1}{2}$OA•d=2|k||2km-m2|=$\frac{|2m|{|m}^{2}{+m}^{4}|}{{(1{-m}^{2})}^{2}}$;…(12分)
∴S△AOB:S△MON=$\frac{4{(m}^{2}{+m}^{4})}{{(1{-m}^{2})}^{2}}$;
令1-m2=t,(t<0),
则S△AOB:S△MON=8${(\frac{1}{t}-\frac{3}{4})}^{2}$-$\frac{1}{2}$>4.…(14分)
∴S△AOB:S△MON的取值范围是(4,+∞).
点评 本题考查了抛物线的定义与几何性质的应用问题,也考查了直线与抛物线的综合应用问题,考查了点到直线的距离以及求三角形的面积的应用问题,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (0,1) | C. | (5,-8) | D. | (-8,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y≥-1 | B. | x≥2 | C. | x+2y+2≥0 | D. | 2x-y+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
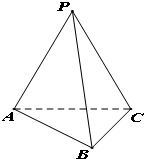 如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.
如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:选择题
如图是某几何体的三视图,图中圆的半径均为1,且俯视图中两条半径互相垂直,则该几何体的体积为( )

A.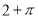 B.
B.
C. D.
D.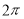
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com