
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
分析 先分析M,N所表示的平面区域,并在平面直角坐标系中用图形表示出来,最后结合平面几何的知识解决问
解答 解:因为f(x)=x2-4x+3=(x-2)2-1,f(y)=(y-2)2-1,
则f(x)+f(y)=(x-2)2+(y-2)2-2,f(x)-f(y)=(x-2)2-(y-2)2.
∴M={(x,y)=(x-2)2+(y-2)2≤2},
N={(x,y)||y-2|≤|x-2|}.
故集合M∩N所表示的平面区域为两个扇形,
其面积为圆面积的一半,即为π.
故选:C.
点评 求限制条件(一般用不等式组来表示)所表示平面区域的面积,一般分为如下步骤:①化简不等式②分析不等式表示的平面区域③画出草图分析可行域④结合平面几何知识求出面积


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$或$\frac{1}{16}$ | C. | $\frac{1}{16}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
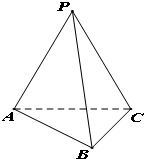 如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.
如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com