
分析 (Ⅰ)由题意,b=1,a2+b2=2c2,结合c2+b2=a2,可求椭圆的标准方程和离心率e;
(Ⅱ)(i)设直线PQ的方程为x=my+n,代入椭圆方程,利用韦达定理,结合kBP•kBQ=e2,求出m,n的关系,即可得出直线PQ过定点M,并求出M点坐标;
(ii)确定P或Q在以BM为直径的圆T,与椭圆方程联立,即可得出结论.
解答 解:(Ⅰ)由题意,b=1,a2+b2=2c2,
∵c2+b2=a2,
∴a2=3,c2=2,
∴$\frac{{x}^{2}}{3}+{y}^{2}=1$,e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$;
(Ⅱ)(i)设直线PQ的方程为x=my+n,设P(x1,y1),Q(x2,y2),
直线方程代入椭圆方程可得(3+m2)y2+2mny+n2-3=0,
∴y1+y2=-$\frac{2mn}{3+{m}^{2}}$,y1y2=$\frac{{n}^{2}-3}{3+{m}^{2}}$,
∴kBP•kBQ=$\frac{{y}_{1}-1}{{x}_{1}}$•$\frac{{y}_{2}-1}{{x}_{2}}$=e2=$\frac{2}{3}$,
整理可得n2-2mn-3m2=0
∴n=-m或n=3m,
∴直线PQ的方程为x=my-m=m(y-1)(舍去)或x=my+3m=m(y+3),
∴直线PQ过定点(0,-3);
(ii)由题意,∠PBQ≠90°,若∠BPM=90°或∠BQM=90°,则P或Q在以BM为直径的圆T上,即在圆x2+(y+1)2=4上,与椭圆方程联立得y=0或1(舍去),
∴P或Q只可以的椭圆的左右顶点,
∴直线PQ的斜率为±$\sqrt{3}$.
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查直线过定点,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},-2)$ | B. | (-1,-1) | C. | $(-\frac{1}{2},-1)$ | D. | (2,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:选择题
已知等差数列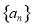 的前
的前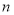 项和为
项和为 ,且
,且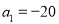 .在区间
.在区间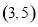 内任取一个实数作为数列
内任取一个实数作为数列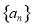 的公差,则
的公差,则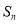 的最小值仅为
的最小值仅为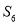 的概率为( )
的概率为( )
A.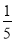 B.
B.
C.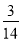 D.
D.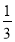
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com