
分析 (Ⅰ)设点P(x,y),通过M、N点坐标,可得$\overrightarrow{MN}$、$\overrightarrow{MP}$、$\overrightarrow{PN}$的坐标表示,利用$\overrightarrow{MN}$•$\overrightarrow{MP}$=$\frac{15}{4}$|$\overrightarrow{PN}$|计算即可;
(Ⅱ)当直线的斜率存在时,设直线方程并代入曲线C中,化简后利用韦达定理计算即得结论;当直线的斜率不存在时,即得结论.
解答 解:(Ⅰ)设点P(x,y),∵M($\frac{9}{2}$,0),N(2,0),
∴$\overrightarrow{MN}$=(-$\frac{5}{2}$,0),$\overrightarrow{MP}$=(x-$\frac{9}{2}$,y),$\overrightarrow{PN}$=(2-x,-y),
代入$\overrightarrow{MN}$•$\overrightarrow{MP}$=$\frac{15}{4}$|$\overrightarrow{PN}$|,化简得$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1,
所以曲线C的方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1;
(Ⅱ)结论:点S是在同一条直线x=$\frac{9}{2}$上.
理由如下:
(1)当直线的斜率存在时,设直线方程为y=k(x-2),
将直线方程代入曲线C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1中,
化简得:(5+9k2)x2-36k2x+(36k2-45)=0.
设点R(x1,y1),Q(x2,y2),利用根与系数的关系得:x1+x2=$\frac{36{k}^{2}}{5+9{k}^{2}}$,x1x2=$\frac{36{k}^{2}-45}{5+9{k}^{2}}$,
在曲线C的方程中令y=0得x=±3,不妨设A(-3,0),B(3,0),
则kBR=$\frac{{y}_{1}}{{x}_{1}-3}$,则直线BR:y=$\frac{{y}_{1}}{{x}_{1}-3}$(x-3).
同理直线$AQ:y=\frac{{y{\;}_2}}{{{x_2}+3}}({x+3})$.
由直线方程BR、AQ,消去y,
得x=$\frac{\frac{3{y}_{1}}{{x}_{1}-3}+\frac{3{y}_{2}}{{x}_{2}+3}}{\frac{{y}_{1}}{{x}_{1}-3}-\frac{{y}_{2}}{{x}_{2}+3}}$=$\frac{6{x}_{1}{x}_{2}+3({x}_{1}+{x}_{2})-18{x}_{2}}{5{x}_{1}{x}_{2}-4{x}_{2}-12}$=$\frac{6•\frac{36{k}^{2}-45}{5+9{k}^{2}}+3•\frac{36{k}^{2}}{5+9{k}^{2}}-18{x}_{2}}{5•\frac{36{k}^{2}-45}{5+9{k}^{2}}-4{x}_{2}-12}$=$\frac{9}{2}$,
所以点S是在直线x=$\frac{9}{2}$上;
(2)当直线的斜率不存在时,则直线方程为x=2.
可得点S的横坐标为$\frac{9}{2}$.
综合(1)(2)得,点S是在同一条直线x=$\frac{9}{2}$上.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
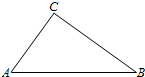 如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
将函数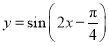 的图象向左平移
的图象向左平移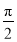 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间 上单调递减 B.在区间
上单调递减 B.在区间 上单调递增
上单调递增
C.在区间 上单调递减 D.在区间
上单调递减 D.在区间 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
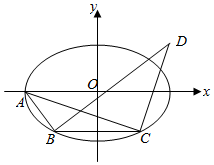 如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com