
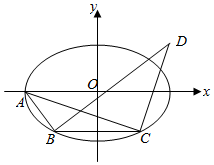
 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$����ΪA����x��ƽ�е�ֱ������ԲE����B��C���㣬��B��C�����ҷֱ���ֱ��AB��AC��ֱ��ֱ���ཻ�ڵ�D����֪��ԲE��������Ϊ$\frac{{\sqrt{5}}}{3}$���ҽ��㵽���ߵľ���Ϊ$\frac{{4\sqrt{5}}}{5}$��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$����ΪA����x��ƽ�е�ֱ������ԲE����B��C���㣬��B��C�����ҷֱ���ֱ��AB��AC��ֱ��ֱ���ཻ�ڵ�D����֪��ԲE��������Ϊ$\frac{{\sqrt{5}}}{3}$���ҽ��㵽���ߵľ���Ϊ$\frac{{4\sqrt{5}}}{5}$������ ��1������$\frac{c}{a}=\frac{{\sqrt{5}}}{3}$��$\frac{a^2}{c}-c=\frac{{4\sqrt{5}}}{5}$�����㼴�ɣ�
��2��ͨ����B��C�����ꡢд��ֱ��AB��AC��BD��CD��б�ʣ�����ֱ��BD��CD�ķ��̣����㼴�ɣ�
��3��ͨ������ɵõ�D�������꣬�����ɵõ�D��ֱ��BC�ľ��룬���������ε������ʽ����������ʽ���ý��ۣ�
��� ��1���⣺�������$\frac{c}{a}=\frac{{\sqrt{5}}}{3}$��$\frac{a^2}{c}-c=\frac{{4\sqrt{5}}}{5}$��
���$a=3��c=\sqrt{5}$��
��b2=a2-c2=4��
����ԲE�ı�����Ϊ$\frac{x^2}{9}+\frac{y^2}{4}=1$��
��2��֤������B��x0��y0����C��-x0��y0������Ȼֱ��AB��AC��BD��CD��б�ʶ����ڣ�
��Ϊk1��k2��k3��k4����${k_1}=\frac{y_0}{{{x_0}+3}}��{k_2}=\frac{y_0}{{-{x_0}+3}}$��${k_3}=-\frac{{{x_0}+3}}{y_0}��{k_4}=\frac{{{x_0}-3}}{y_0}$��
��ֱ��BD��CD�ķ���Ϊ��$y=-\frac{{{x_0}+3}}{y_0}��x-{x_0}��+{y_0}��y=\frac{{{x_0}-3}}{y_0}��x+{x_0}��+{y_0}$��
��ȥy�ã�$-\frac{{{x_0}+3}}{y_0}��x-{x_0}��+{y_0}=\frac{{{x_0}-3}}{y_0}��x+{x_0}��+{y_0}$��
�����x=3���ʵ�D�ڶ�ֱ��x=3���˶���
��3���⣺�ɣ�2���õ�D��������Ϊ${y_D}=\frac{{{x_0}-3}}{y_0}��3+{x_0}��+{y_0}=\frac{x_0^2-9}{y_0}+{y_0}$��
�֡�$\frac{x_0^2}{9}+\frac{y_0^2}{4}=1$����$x_0^2-9=-\frac{9y_0^2}{4}$��
��${y_D}=\frac{{{x_0}-3}}{y_0}��3+{x_0}��+{y_0}=\frac{{-\frac{9}{4}y_0^2}}{y_0}+{y_0}=-\frac{5}{4}{y_0}$��
���D��ֱ��BC�ľ���h=$|{{y_D}-{y_0}}|=|{-\frac{5}{4}{y_0}-{y_0}}|=\frac{9}{4}|{y_0}|$��
��y=y0����$\frac{x^2}{9}+\frac{y^2}{4}=1$����$x=��3\sqrt{1-\frac{y_0^2}{4}}$��
���BCD���${S_{��ABC}}=\frac{1}{2}BC•h=\frac{1}{2}��6\sqrt{1-\frac{y_0^2}{4}}•\frac{9}{4}|{y_0}|$
=$\frac{27}{2}\sqrt{1-\frac{y_0^2}{4}}•\frac{1}{2}|{y_0}|��\frac{27}{2}•\frac{{1-\frac{y_0^2}{4}+\frac{y_0^2}{4}}}{2}=\frac{27}{4}$��
���ҽ���$1-\frac{y_0^2}{4}=\frac{y_0^2}{4}$����${y_0}=��\sqrt{2}$ʱ�Ⱥų�����
��${y_0}=��\sqrt{2}$ʱ����BCD��������ֵΪ$\frac{27}{4}$��
���� ���⿼����Բ�Ķ��弰������̡�ֱ������Բ��λ�ù�ϵ�������ε��������Ȼ���֪ʶ�������������������ע����ⷽ���Ļ��ۣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ׯ���и���9���¿���ѧ���ģ��Ծ��������棩 ���ͣ�ѡ����
ij����������ͼ��ͼ��ʾ����ü���������Ϊ������ͼ�л�����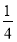 Բ������ ��
Բ������ ��
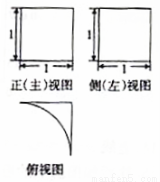
A��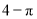 B��
B��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ׯ���и���9���¿���ѧ�������Ծ��������棩 ���ͣ������
��֪ż����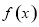 ��
�� ������������������
������������������ ��ʵ��
��ʵ�� ��ȡֵ��Χ��______________��
��ȡֵ��Χ��______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ׯ���и���9���¿���ѧ�������Ծ��������棩 ���ͣ�ѡ����
ij����������ͼ��ͼ��ʾ����ü���������Ϊ������ͼ�л�����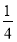 Բ������ ��
Բ������ ��

A�� B��
B��
C��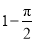 D��
D��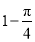
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1����2�� | B�� | ��1����3�� | C�� | ��2����3�� | D�� | ��1����2����3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=$\frac{��}{2}$ | B�� | x=�� | C�� | x=$\frac{��}{6}$ | D�� | x=$\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��������ABCD-A1B1C1D1�У�AA1��ƽ��A1B1C1D1������A1B1C1D1�DZ߳�Ϊa�������Σ�����AA1�ij�Ϊb��EΪ����BB1�ϵĶ��㣨�����˵㣩��������
��������ABCD-A1B1C1D1�У�AA1��ƽ��A1B1C1D1������A1B1C1D1�DZ߳�Ϊa�������Σ�����AA1�ij�Ϊb��EΪ����BB1�ϵĶ��㣨�����˵㣩��������| A�� | �������a��b�����ڵ�E��ʹ��B1D��EC1 | |
| B�� | ���ҽ���a=bʱ�����ڵ�E��ʹ��B1D��EC1 | |
| C�� | ���ҽ���a��bʱ�����ڵ�E��ʹ��B1D��EC1 | |
| D�� | ���ҽ���a��bʱ�����ڵ�E��ʹ��B1D��EC1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com