
分析 由题意可得动直线y=k(x-$\sqrt{2}$)过定点($\sqrt{2}$,0),曲线y=$\sqrt{1-{x^2}}$表示单位圆x2+y2=1的上半圆,可得当∠AOB=$\frac{π}{2}$时,S△AOB面积最大,由点到直线的距离公式可得k的方程,解方程可得.
解答 解:由题意可得动直线y=k(x-$\sqrt{2}$)过定点($\sqrt{2}$,0),
曲线y=$\sqrt{1-{x^2}}$表示单位圆x2+y2=1的上半圆,
∵△AOB的面积S=$\frac{1}{2}$|OA||OB|sin∠AOB=$\frac{1}{2}$×1×1×sin∠AOB,
当∠AOB=$\frac{π}{2}$时,S△AOB面积最大.
此时O到AB的距离d=$\frac{\sqrt{2}}{2}$.
直线AB方程可化为即kx-y-$\sqrt{2}$k=0,k<0
由距离公式可得$\frac{|-\sqrt{2}k|}{\sqrt{{k}^{2}+1}}$=$\frac{\sqrt{2}}{2}$,解得k=$-\frac{{\sqrt{3}}}{3}$,
故答案为:$-\frac{{\sqrt{3}}}{3}$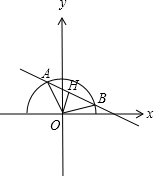
点评 本题考查直线和圆的位置关系,涉及三角形的面积公式和数形结合的思想,属中档题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
将函数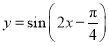 的图象向左平移
的图象向左平移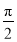 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间 上单调递减 B.在区间
上单调递减 B.在区间 上单调递增
上单调递增
C.在区间 上单调递减 D.在区间
上单调递减 D.在区间 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
如图,在四棱锥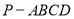 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, .
.

(1)在 上确定一点
上确定一点 ,使得
,使得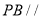 平面
平面 ,并求
,并求 的值;
的值;
(2)在(1)条件下,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com