
分析 设a+b=t,得b=t-a,代入a2-2ab+5b2=4后化为关于a的一元二次方程,由a有实根得判别式大于等于0,转化为关于t的不等式得答案.
解答 解:设a+b=t,则b=t-a,
代入a2-2ab+5b2=4,得a2-2a(t-a)+5(t-a)2-4=0,
整理得:8a2-12at+5t2-4=0.
由△=(-12t)2-32(5t2-4)≥0,得t2≤8.
即$-2\sqrt{2}≤t≤2\sqrt{2}$.
∴a+b的取值范围为$[{-2\sqrt{2},2\sqrt{2}}]$.
故答案为:$[{-2\sqrt{2},2\sqrt{2}}]$.
点评 本题给出关于正数a、b的等式,求a+b的最小值.考查了利用换元法和一元二次方程有实根求解参数范围问题,考查数学转化思想方法,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{2}$ | B. | x=π | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},-2)$ | B. | (-1,-1) | C. | $(-\frac{1}{2},-1)$ | D. | (2,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 |
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲
设函数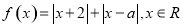 .
.
(1)若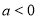 ,且
,且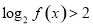 对任意
对任意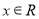 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)若 ,且关于
,且关于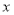 的不等式
的不等式 有解,求实数
有解,求实数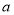 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com