
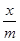 )定义域为{x|0<x<m
)定义域为{x|0<x<m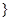 。
。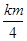 .
.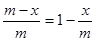 。
。 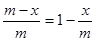 ,依题意,鱼群增长量为y=kx(1-
,依题意,鱼群增长量为y=kx(1-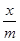 ),
), 。
。 当x=m/2时,
当x=m/2时,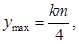

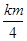 .
. ,得-2<k<2,但k>0,
,得-2<k<2,但k>0,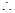 0<k<2.
0<k<2.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:不详 题型:解答题
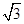 、圆心角为
、圆心角为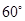 的扇形的弧上任取一点
的扇形的弧上任取一点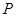 ,作扇形的内接矩形
,作扇形的内接矩形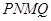 ,使点
,使点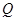 在
在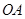 上,点
上,点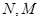 在
在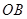 上,设矩形
上,设矩形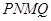 的面积为
的面积为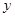 ,
,
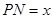 ,将
,将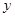 表示成
表示成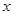 的函数关系式;
的函数关系式;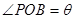 ,将
,将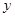 表示成
表示成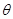 的函数关系式;
的函数关系式;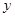 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
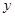 万元与投入
万元与投入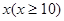 万元之间满足:
万元之间满足: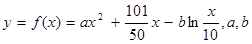 为常数。当
为常数。当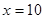 万元时,
万元时,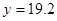 万元;
万元;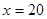 万元时,
万元时,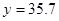 万元。 (参考数据:
万元。 (参考数据: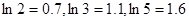 )
)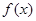 的解析式;
的解析式;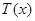 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
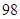 万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出
万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出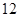 万元,第二年需要支出
万元,第二年需要支出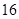 万元,第三年需要支出
万元,第三年需要支出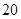 万元,……,每年都比上一年增加支出
万元,……,每年都比上一年增加支出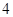 万元,而每年的生产收入都为
万元,而每年的生产收入都为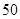 万元.假设这套生产设备投入使用
万元.假设这套生产设备投入使用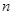 年,
年,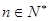 ,生产成本等于生产设备购置费与这
,生产成本等于生产设备购置费与这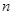 年生产产品相关的各种配套费用的和,生产总利润
年生产产品相关的各种配套费用的和,生产总利润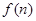 等于这
等于这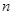 年的生产收入与生产成本的差. 请你根据这些信息解决下列问题:
年的生产收入与生产成本的差. 请你根据这些信息解决下列问题: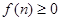 ,求
,求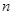 的值;
的值;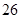 万元的价格出售该套设备;
万元的价格出售该套设备;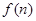 取得最大值时,以
取得最大值时,以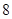 万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
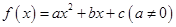 ,且不等式
,且不等式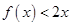 的解集为
的解集为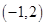 .
.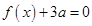 有两个相等的实根,求
有两个相等的实根,求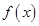 的解析式;
的解析式;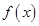 的最小值不大于
的最小值不大于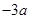 ,求实数
,求实数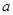 的取值范围;
的取值范围;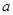 如何取值时,函数
如何取值时,函数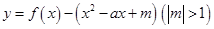 存在零点,并求出零点.
存在零点,并求出零点.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
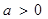 ,函数
,函数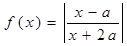 。
。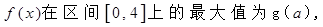 求
求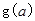 的表达式;
的表达式;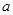 ,使函数
,使函数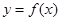 在区间
在区间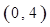 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求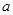 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com