
如图,已知曲线 ,曲线
,曲线 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与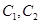 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.

(1)在正确证明 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线 与
与 有公共点,求证
有公共点,求证 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆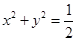 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
见解析
【解析】(1)C1的左焦点为 ,过F的直线
,过F的直线 与C1交于
与C1交于 ,与C2交于
,与C2交于 ,故C1的左焦点为“C1-C2型点”,且直线可以为
,故C1的左焦点为“C1-C2型点”,且直线可以为 ;
;
(2)直线 与C2有交点,则
与C2有交点,则
 ,若方程组有解,则必须
,若方程组有解,则必须 ;
;
直线 与C2有交点,则
与C2有交点,则
 ,若方程组有解,则必须
,若方程组有解,则必须
故直线 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”。
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”。
(3)显然过圆 内一点的直线
内一点的直线 若与曲线C1有交点,则斜率必存在;
若与曲线C1有交点,则斜率必存在;
根据对称性,不妨设直线 斜率存在且与曲线C2交于点
斜率存在且与曲线C2交于点 ,则
,则

直线 与圆
与圆 内部有交点,故
内部有交点,故
化简得, ①
①
若直线 与曲线C1有交点,则
与曲线C1有交点,则


化简得, ②
②
由①②得,
但此时,因为 ,即①式不成立;
,即①式不成立;
当 时,①式也不成立
时,①式也不成立
综上,直线 若与圆
若与圆 内有交点,则不可能同时与曲线C1和C2有交点,
内有交点,则不可能同时与曲线C1和C2有交点,
即圆 内的点都不是“C1-C2型点” .
内的点都不是“C1-C2型点” .
【考点定位】考查双曲线,直线,圆的位置关系,综合性较强,属难题。


科目:高中数学 来源: 题型:
 (2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.
(2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知曲线C:y=
如图,已知曲线C:y=| 1 |
| x |
| 4 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•黄冈模拟)如图,已知曲线c1:
(2009•黄冈模拟)如图,已知曲线c1:| x2 |
| a2 |
| y2 |
| b 2 |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).
如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).| 7 | 9 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌三中高二(下)期中数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com