解:(I)已知函数定义域为(0,+∝),
又有a>0,则y
2=-

是增函数,
y
1=lnx与y
2=-

都是增函数,
故f(x)=lnx-

在定义域上是增函数.
(Ⅱ)由已知f(x)<x
2,即f(x)=lnx-

<x
2,在(1,+∞)上恒成立,
即a>xlnx-x
3在(1,+∞)上恒成立
令g(x)=xlnx-x
3,则g′(x)=lnx-3x
2+1,
又[g′(x)]'=
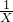
-6x<0,在(1,+∞)上恒成立,
所以g′(x)在(1,+∞)上为减函数,故g′(x)<g′(1)<0,
因此g(x)在(1,+∞)为减函数,
故a≥g(1),即a≥-1.
(III)分三种情况讨论,
(1)令f′(x)≥0,在[1,e]上恒成立,x+a≥0,即a≥-x,
则a≥-1时.此时f(x)在[1,e]上为增函数.
f(x)
min=f(1)=-a=

,
得a=-

,(舍去)
(2)令f′(x)≤0,在[1,e]上恒成立,有x+a≤0,即a≤-x,
则a≤-e时.此时f(x)在[1,e]上为减函数.
则f(x)
min=f(e)=1-

=

,
得a=-

(舍去),
(3)当-e<x<-1时,令f′(x)=0,得x
0=-a,
当1<x<x
0时,f′(x)<0,f(x)在(1,x
0)上为减函数,
当x
0<x<e时,f′(x)>0,f(x)在(x
0,e)上为增函数,
f(x)
min=f(-a)=ln(-a)+1=

,
解可得a=-

,
综上可得,a=-

..
分析:(I)根据题意,易得函数的定义域,将原函数分为两部分,即y
1=lnx与y
2=-

,易得两者均为增函数,进而由单调性的性质,可得f(x)的单调性;
(Ⅱ)分析可得,f(x)<x
2恒成立等价于a>xlnx-x
3在(1,+∞)上恒成立,令g(x)=xlnx-x
3,对其求导,可以判断其为减函数,进而可得其最大值,另a大于其最大值可得答案;
(III)根据题意,对函数的定义域分三种情况讨论,分别求导,判断单调性,求出最小值,令其等于

,可以解得a的值,分析取舍可得答案.
点评:本题考查导函数的运用,一般方法为先求导,再分析单调性,进而分析可得函数的极值,比较可得函数的最值;注意有时需要对函数的极值或已知区间分情况讨论.

 .
. ,求a的值.
,求a的值. 是增函数,
是增函数, 都是增函数,
都是增函数, 在定义域上是增函数.
在定义域上是增函数. <x2,在(1,+∞)上恒成立,
<x2,在(1,+∞)上恒成立,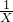 -6x<0,在(1,+∞)上恒成立,
-6x<0,在(1,+∞)上恒成立, ,
, ,(舍去)
,(舍去) =
= ,
, (舍去),
(舍去), ,
, ,
, ..
.. ,易得两者均为增函数,进而由单调性的性质,可得f(x)的单调性;
,易得两者均为增函数,进而由单调性的性质,可得f(x)的单调性; ,可以解得a的值,分析取舍可得答案.
,可以解得a的值,分析取舍可得答案.
