
【题目】近几年,电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务,该配送站有8名新手快递员和4名老快递员,但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹,日工资320元;每个老快递员每天可配送300件包裹,日工资520元.
(Ⅰ)求该配送站每天需支付快递员的总工资最小值;
(Ⅱ)该配送站规定:新手快递员某个月被评为“优秀”,则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”,日工资会超过老快递员?
(参考数据: ![]() ,
, ![]() ,
, ![]() .)
.)
【答案】(1) 该配送站每天需支付快递员的总工资最小值为2560元;(2) 新手快递员至少连续5 个月被评为“优秀”,日工资会超过老快递员.
【解析】试题分析:(Ⅰ)本题属于线性规划问题,设安排新手快递员![]() 人,老快递员
人,老快递员![]() 人,可得约束条件和目标函数,画出可行域,经过平移直线
人,可得约束条件和目标函数,画出可行域,经过平移直线![]() 可得最优解为
可得最优解为![]() ,求得
,求得![]() 元。(Ⅱ) 设新手快递员连续
元。(Ⅱ) 设新手快递员连续![]() 个月被评为“优秀”,日工资会超过老员工,则由题意可得
个月被评为“优秀”,日工资会超过老员工,则由题意可得![]() .整理得
.整理得![]() ,两边取对数可解得
,两边取对数可解得![]() ,所以
,所以![]() 的最小值为5.
的最小值为5.
试题解析:
(Ⅰ)设安排新手快递员![]() 人,老快递员
人,老快递员![]() 人,
人,
由题意得 ,即
,即 ,
,
该配送站每天需支付快递员总工资为![]() .
.
作出不等式组表示的可行域如图所示.

作直线![]() ,平移直线
,平移直线![]() 可得到一组与之平行的直线
可得到一组与之平行的直线![]() .
.
由题设![]() 是可行域内的整点的横、纵坐标.
是可行域内的整点的横、纵坐标.
在可行域内的整点中,点![]() 使
使![]() 取得最小值,
取得最小值,
即当![]() 过点
过点![]() 时,
时, ![]() 取得最小值,且
取得最小值,且![]() (元).
(元).
即该配送站每天需支付快递员的总工资最小值为2560元
(Ⅱ)设新手快递员连续![]() 个月被评为“优秀”,日工资会超过老员工.
个月被评为“优秀”,日工资会超过老员工.
则由题意可得![]() .
.
整理得![]() ,
,
两边取对数可得![]() ,
,
所以![]()
![]() ,
,
又因为![]() ,所以
,所以![]() 的最小值为5.
的最小值为5.
即新手快递员至少连续5 个月被评为“优秀”,日工资会超过老快递员.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】(Ⅰ)已知集合A={(x,y)|y=x2+2},B={(x,y)|y=6﹣x2},求A∩B; (Ⅱ)已知集合A={y|y=x2+2},B={y|y=6﹣x2},求A∩B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. 将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图象
的图象
B. 函数![]() 图象关于点
图象关于点![]() 中心对称
中心对称
C. 函数![]() 的图象关于
的图象关于![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内单调递增
内单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P:(x﹣a)2+(y﹣b)2=r2(r>0)被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于 ![]() (其中P(a,b)为圆心,O为坐标原点).
(其中P(a,b)为圆心,O为坐标原点).
(1)求a,b所满足的关系式;
(2)点P在直线x﹣2y=0上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在△POA内”的概率的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图ABCD﹣A1B1C1D1是长方体,O是B1D1的中点,直线AC1交平面CB1D1于点M,则下列结论正确的是( ) 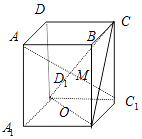
A.C,M,O三点共线
B.C,M,O,A1不共面
C.A,M,O,C不共面
D.B,M,O,B1共面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com