
| A. | -1 | B. | 4 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
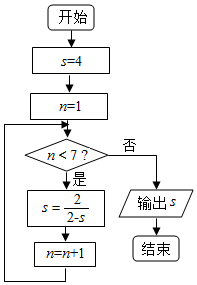
分析 由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:当t=1时,满足进行循环的条件,S=$\frac{2}{2-4}$=-1,t=2;
当t=2时,满足进行循环的条件,S=$\frac{2}{2-(-1)}$=$\frac{2}{3}$,t=3;
当t=3时,满足进行循环的条件,S=$\frac{2}{2-\frac{2}{3}}$=$\frac{3}{2}$,t=4;
当t=4时,满足进行循环的条件,S=$\frac{2}{2-\frac{3}{2}}$=4,t=5;
当t=5时,满足进行循环的条件,S=$\frac{2}{2-4}$=-1,t=6;
当t=6时,满足进行循环的条件,S=$\frac{2}{2-(-1)}$=$\frac{2}{3}$,t=7;
当t=7时不满足进行循环的条件,
此时S值为$\frac{2}{3}$,
故选:D.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$或$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
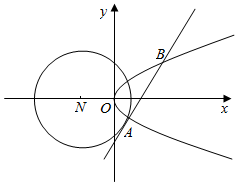 如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
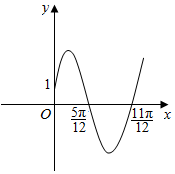 函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).
函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com