
分析 (1)由等差数列的性质可得:a5+a16=20=a1+a20.利用S20=$\frac{20({a}_{1}+{a}_{20})}{2}$即可得出.
(2)由题意可得:a1+a2+a3+a4=25,an-3+an-2+an-1+an=63,可得4(a1+an)=63+25=88,解得a1+an.利用Sn=275=$\frac{n({a}_{1}+{a}_{n})}{2}$即可得出.
解答 解:(1)由等差数列的性质可得:a5+a16=20=a1+a20.
∴S20=$\frac{20({a}_{1}+{a}_{20})}{2}$=10×20=200.
(2)由题意可得:a1+a2+a3+a4=25,an-3+an-2+an-1+an=63,
∴4(a1+an)=63+25=88,解得a1+an=22.
∴Sn=275=$\frac{n({a}_{1}+{a}_{n})}{2}$=$\frac{n×22}{2}$.
解得n=25.
点评 本题考查了等差数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2016-2017学年河南八市高二文上月考一数学试卷(解析版) 题型:选择题
设 ,在约束条件
,在约束条件 下,目标函数
下,目标函数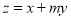 的最大值小于2,则
的最大值小于2,则 的取值范围为( )
的取值范围为( )
A. B.
B.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍 (纵坐标不变) | |
| B. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:
如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com