
分析 (1)根据直线方程求出直线的斜率和倾斜角的正切值,利用两角和差的正切公式结合同角的三角函数的关系进行求解即可,
(2)根据(1)的结论,结合辅助角公式化简f(x),利用五点法进行作图即可.
解答 解:(1)直线y=7x的斜率为7,设倾斜角为α,则tanα=7,α为第一象限角,
将直线y=7x绕着原点逆时针旋转$\frac{π}{4}$后对应直线的倾斜角为α+$\frac{π}{4}$,
则斜率tan(α+$\frac{π}{4}$)=$\frac{tanα+tan\frac{π}{4}}{1-tanαtan\frac{π}{4}}$=$\frac{7+1}{1-7×1}$=$\frac{8}{-6}$=-$\frac{4}{3}$,
∵旋转$\frac{π}{4}$后所得的直线过点A(cosθ,sinθ)
∴tan(α+$\frac{π}{4}$)=$\frac{sinθ}{cosθ}$=tanθ=-$\frac{4}{3}$,
∵tanθ=tan(α+$\frac{π}{4}$)=-$\frac{4}{3}$<0,
∴θ为第二象限角,或第四象限,
若θ为第二象限角,则sinθ>0,cosθ<0,
由$\left\{\begin{array}{l}{tanθ=-\frac{4}{3}}\\{sin^2θ+cos^2θ=1}\end{array}\right.$得$\left\{\begin{array}{l}{sinθ=\frac{4}{5}}\\{cosθ=-\frac{3}{5}}\end{array}\right.$,
即sinθ=$\frac{4}{5}$,cosθ=-$\frac{3}{5}$,tanθ=-$\frac{4}{3}$;
若θ为第四象限角,则sinθ<0,cosθ>0,
由$\left\{\begin{array}{l}{tanθ=-\frac{4}{3}}\\{sin^2θ+cos^2θ=1}\end{array}\right.$得$\left\{\begin{array}{l}{sinθ=-\frac{4}{5}}\\{cosθ=\frac{3}{5}}\end{array}\right.$,
即sinθ=-$\frac{4}{5}$,cosθ=$\frac{3}{5}$,tanθ=-$\frac{4}{3}$;
(2)若点A位于第二象限,由(1)知sinθ=$\frac{4}{5}$,cosθ=-$\frac{3}{5}$,
∴f(x)=$\frac{5\sqrt{3}}{2}$sinθcosx+$\frac{10}{3}$cosθsinx=$\frac{5\sqrt{3}}{2}$×$\frac{4}{5}$cosx-$\frac{3}{5}$×$\frac{10}{3}$sinx
=2$\sqrt{3}$cosx-2sinx=4cos(x+$\frac{π}{6}$),
(2)用五点作图法作出f(x)的简图.
当x∈[$\frac{π}{3}$,$\frac{7π}{3}$],则x+$\frac{π}{6}$∈[$\frac{π}{2}$,$\frac{5π}{2}$]
列表:
| x+$\frac{π}{6}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{5π}{2}$ |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ |
| 4cos(x+$\frac{π}{6}$) | 0 | -4 | 0 | 4 | 0 |
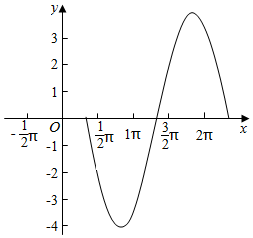
点评 本题主要考查三角函数的图象和性质,利用条件求出函数的解析式是解决本题的关键.要求熟练掌握五点作图法.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
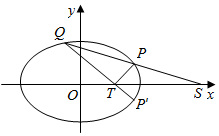 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为(-2,0),离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为(-2,0),离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com