
分析 根据函数奇偶性和单调性的关系,将不等式进行转化进行求解即可.
解答 解:∵f(x)是定义在R上的偶函数,
∴不等式f(lnx)<l等价为f(|lnx|)<l,
当x≥0时,f(x)=$\frac{2x-3}{x+1}$=$\frac{2(x+1)-5}{x+1}$=2-$\frac{5}{x+1}$,则函数f(x)为增函数,
由f(x)=$\frac{2x-3}{x+1}$=1,得x=4,即f(4)=1,
则不等式f(|lnx|)<l等价为f(|lnx|)<f(4),
则|lnx|<4,
即-4<lnx<4,
即$\frac{1}{{e}^{4}}$<x<e4,
即不等式的解集为($\frac{1}{{e}^{4}}$,e4),
故答案为:($\frac{1}{{e}^{4}}$,e4)
点评 本题主要考查不等式的求解,根据条件判断函数的单调性,利用函数单调性和奇偶性的关系将不等式进行转化是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{4}$,$\frac{1}{3}$] | B. | [$\frac{1}{4}$,$\frac{1}{3}$) | C. | [$\frac{1}{5}$,$\frac{1}{3}$) | D. | [$\frac{1}{5}$,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
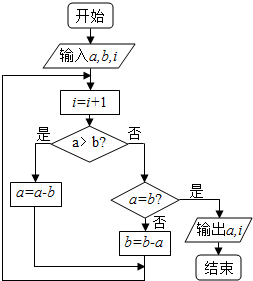 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )| A. | 0,3 | B. | 0,4 | C. | 2,3 | D. | 2,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
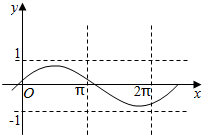
| A. | f(x)=$\frac{3}{4}$sin($\frac{3}{2}$x+$\frac{π}{6}$) | B. | f(x)=$\frac{4}{5}$sin($\frac{4}{5}$x+$\frac{1}{5}$) | C. | f(x)=$\frac{4}{5}$sin($\frac{5}{6}$x+$\frac{π}{6}$) | D. | f(x)=$\frac{4}{5}$sin($\frac{2}{3}$x-$\frac{1}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%的把握认为“X和Y有关系” | B. | 有95%的把握认为“X和Y没有关系” | ||
| C. | 有99%的把握认为“X和Y有关系” | D. | 有99%的把握认为“X和Y没有关系” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com