
【题目】设函数![]() ,若
,若![]() 在区间
在区间![]() 上无零点,则实数
上无零点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】函数f(x)=ln(x+1)+a(x2﹣x),其中a∈R,x∈(﹣1,+∞).
f′(x)=![]() ,
,
令g(x)=2ax2+ax﹣a+1.
(i)当a=0时,g(x)=1,此时f′(x)>0,函数f(x)在(0,+∞)上单调递增(ii)当a>0时,△=a2﹣8a(1﹣a)=a(9a﹣8).
①当0<a≤![]() 时,△≤0,g(x)≥0,f′(x)≥0,函数f(x)在(0,+∞)上单调递增,无极值点.
时,△≤0,g(x)≥0,f′(x)≥0,函数f(x)在(0,+∞)上单调递增,无极值点.
②当a>![]() 时,△>0,设方程2ax2+ax﹣a+1=0的两个实数根分别为x1,x2,x1<x2.
时,△>0,设方程2ax2+ax﹣a+1=0的两个实数根分别为x1,x2,x1<x2.
当x∈(﹣1,x1)时,g(x)>0,f′(x)>0,函数f(x)单调递增;
当x∈(x1,x2)时,g(x)<0,f′(x)<0,函数f(x)单调递减;
当x∈(x2,+∞)时,g(x)>0,f′(x)>0,函数f(x)单调递增.
①当0≤a≤![]() 时,函数f(x)在(0,+∞)上单调递增.
时,函数f(x)在(0,+∞)上单调递增.
∵f(0)=0,
∴x∈(0,+∞)时,f(x)>0,符合题意.
②当 ![]() <a≤1时,由g(0)≥0,可得x2≤0,函数f(x)在(0,+∞)上单调递增.
<a≤1时,由g(0)≥0,可得x2≤0,函数f(x)在(0,+∞)上单调递增.
又f(0)=0,
∴x∈(0,+∞)时,f(x)>0.
③当1<a时,由g(0)<0,可得x2>0,
∴x∈(0,x2)时,函数f(x)单调递减.
又f(0)=0,∴x∈(0,x2)时,f(x)<0,x趋向于正无穷时函数值大于0,不符合题意,舍去;
④当a<0时,设h(x)=x﹣ln(x+1),x∈(0,+∞),h′(x)=![]() >0.
>0.
∴h(x)在(0,+∞)上单调递增.
因此x∈(0,+∞)时,h(x)>h(0)=0,即ln(x+1)<x,
可得:f(x)<x+a(x2﹣x)=ax2+(1﹣a)x,
当x>1﹣![]() 时,
时,
ax2+(1﹣a)x<0,此时f(x)<0,不合题意,舍去.
综上所述,a的取值范围为[0,1].
故答案为:A.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
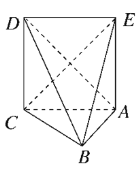
【题目】如图,在三棱锥D-ABC中,![]() 底面ABC,
底面ABC,![]() 为正三角形,若
为正三角形,若![]() ,
,![]() ,则三棱锥D-ABC与三棱锥E-ABC的公共部分构成的几何体的外接球的体积为( )
,则三棱锥D-ABC与三棱锥E-ABC的公共部分构成的几何体的外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念五四运动100周年和建团97周年,某校团委开展“青春心向党,建功新时代”知识问答竞赛.在小组赛中,甲乙丙3人进行擂台赛,每局2人进行比赛,另1人当裁判,每一局的输方担任下局的裁判,由原来裁判向胜者挑战,甲乙丙3人实力相当.
(1)若第1局是由甲担任裁判,求第4局仍是甲担任裁判的概率;
(2)甲乙丙3人进行的擂台赛结束后,经统计,甲共参赛了6局,乙共参赛了5局而丙共担任了2局裁判.则甲乙丙3人进行的擂台赛共进行了多少局?若从小组赛中,甲乙丙比赛的所有场次中任取2场,则均是由甲担任裁判的概率是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com