
分析 (1)$\overrightarrow{AB}+\overrightarrow{AC}$可根据向量加法的平行四边形法则作出:可取BC边上的中点D,连接AD并延长到E,使得AD=DE,从而有$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AE}$,根据条件便可得到$\overrightarrow{AP}=λ\overrightarrow{AE}$,AE过△ABC的重心,从而得出P的轨迹过△ABC的重心;
(2)可分别作作$\overrightarrow{AD}=\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,$\overrightarrow{AE}=\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,并以AD,AE为邻边作?ADFE,从而可得到$\overrightarrow{AP}=λ\overrightarrow{AF}$,而线段AF在∠BAC的平分线上,从而便得出P的轨迹过△ABC的内心;
(3)可作AD⊥BC,则可得到$\overrightarrow{AP}=\frac{λ}{|AD|}(\overrightarrow{AB}+\overrightarrow{AC})$,这样就和(1)一样了,从而轨迹也过重心;
(4)作AD⊥BC,求$\overrightarrow{BC}•\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}=-|\overrightarrow{BC}|$,而同样有$\overrightarrow{BC}•\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}=|\overrightarrow{BC}|$,这样即可得到$\overrightarrow{BC}•\overrightarrow{AP}=0$,从而得出P的轨迹过△ABC的垂心.
解答 解:(1)如图,取BC中点D,连接AD并延长到E,使AD=DE,则$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AE}$;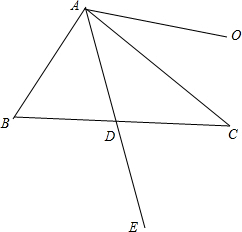 ∴由$\overrightarrow{OP}=\overrightarrow{OA}+λ(\overrightarrow{AB}+\overrightarrow{AC})$得:
∴由$\overrightarrow{OP}=\overrightarrow{OA}+λ(\overrightarrow{AB}+\overrightarrow{AC})$得:
$\overrightarrow{AP}=λ\overrightarrow{AE}$,λ≥0;
∴$\overrightarrow{AP}$与$\overrightarrow{AE}$同向,∴P在射线AE上;
AE过△ABC的重心,∴P的轨迹一定过△ABC的重心;
(2)$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$表示和$\overrightarrow{AB}$方向相同的单位向量,$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$表示和$\overrightarrow{AC}$方向相同的单位向量,如图所示: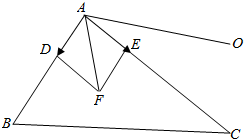 作$\overrightarrow{AD}=\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,$\overrightarrow{AE}=\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,以AD,AE为邻边作?ADFE,则:
作$\overrightarrow{AD}=\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$,$\overrightarrow{AE}=\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,以AD,AE为邻边作?ADFE,则:
$\overrightarrow{AD}+\overrightarrow{AE}=\overrightarrow{AF}$;
∴由$\overrightarrow{OP}=\overrightarrow{OA}+λ(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|})$得:$\overrightarrow{AP}=λ\overrightarrow{AF}$;
∵λ≥0;
∴P点在射线AF上,AF在∠BAC的平分线上;
∴P点的轨迹过△ABC的内心;
(3)如图,过A作AD⊥BC,则: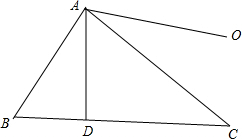 $|\overrightarrow{AB}|sinB=|\overrightarrow{AD}|,|\overrightarrow{AC}|sinC=|\overrightarrow{AD}|$;
$|\overrightarrow{AB}|sinB=|\overrightarrow{AD}|,|\overrightarrow{AC}|sinC=|\overrightarrow{AD}|$;
∴$\overrightarrow{OP}=\overrightarrow{OA}+λ(\frac{\overrightarrow{AB}}{|\overrightarrow{AD}|}+\frac{\overrightarrow{AC}}{|\overrightarrow{AD}|})$;
∴$\overrightarrow{AP}=\frac{λ}{|\overrightarrow{AD}|}(\overrightarrow{AB}+\overrightarrow{AC})$;
这样就变成了(1);
∴P点的轨迹一定过△ABC的重心;
(4)如图,作AD⊥BC,垂足为D,则: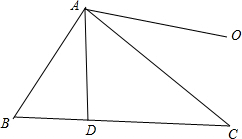 $\overrightarrow{BC}•\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}=\frac{|\overrightarrow{BC}||\overrightarrow{AB}|cos(π-B)}{|\overrightarrow{AB}|cosB}$=$-|\overrightarrow{BC}|$;
$\overrightarrow{BC}•\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}=\frac{|\overrightarrow{BC}||\overrightarrow{AB}|cos(π-B)}{|\overrightarrow{AB}|cosB}$=$-|\overrightarrow{BC}|$;
同理$\overrightarrow{BC}•\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}=|\overrightarrow{BC}|$;
∴由$\overrightarrow{OP}=\overrightarrow{OA}+λ(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC})$得:
$\overrightarrow{AP}=λ(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC})$;
∴$\overrightarrow{AP}•\overrightarrow{BC}=λ(-|\overrightarrow{BC}|+|\overrightarrow{BC}|)=0$;
∴$\overrightarrow{AP}⊥\overrightarrow{BC}$;
∴P点在射线AD上,AD为△ABC的高线;
∴P的轨迹一定过△ABC的垂心.
故答案为:重心,内心,重心,垂心.
点评 考查向量加法的平行四边形法则,共线向量基本定理,三角形重心、内心,及垂心的定义,单位向量的定义,正弦函数的定义,以及数量积的计算公式,向量垂直的充要条件.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | $\sqrt{D(ξ)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
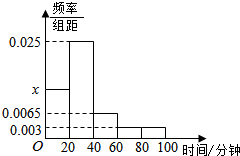 古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].
古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com