
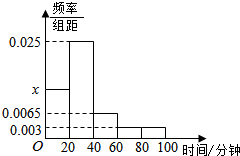
 ������˵�ĺã��������лƽ��ݣ������������������Ķ��Դ�ѧ��������һ������Ч������ѧϰ��ʽ��ij��ѧ�Ա�У��һѧ�������˿����Ķ���״�ĵ��飬�ӵ����з��ִ�һѧ��ƽ��ÿ������Ķ�ʱ��ķ�Χ��[0��100]����λ�����ӣ��������õ�ƽ��ÿ������Ķ�ʱ������ݻ��Ƴ�ƽ�ʷֲ�ֱ��ͼ����ͼ�����������ݷ���Ϊ[0��20����[20��40����[60��80����[80��100]��
������˵�ĺã��������лƽ��ݣ������������������Ķ��Դ�ѧ��������һ������Ч������ѧϰ��ʽ��ij��ѧ�Ա�У��һѧ�������˿����Ķ���״�ĵ��飬�ӵ����з��ִ�һѧ��ƽ��ÿ������Ķ�ʱ��ķ�Χ��[0��100]����λ�����ӣ��������õ�ƽ��ÿ������Ķ�ʱ������ݻ��Ƴ�ƽ�ʷֲ�ֱ��ͼ����ͼ�����������ݷ���Ϊ[0��20����[20��40����[60��80����[80��100]������ ��1������Ƶ�ʷֲ�ֱ��ͼ�и���֮��Ϊ1�����������x��ֵ��
��2������֪��X��B��4��0.31�����ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ���ã�
��0.003��2+0.0065+x+0.025����20=1��
���x=0.0125��
��2����Ƶ�ʷֲ�ֱ��ͼ����1���ô�һѧ��ƽ��ÿ������Ķ�ʱ������20���ӵĸ���Ϊ0.0155��20=0.31��
��X��B��4��0.31����
P��X=0��=${C}_{4}^{0}��0.69��^{4}$=0.22667121��
P��X=1��=${C}_{4}^{1}��0.31��0.6{9}^{3}$=0.40735116��
P��X=2��=${C}_{4}^{2}��0.3{1}^{2}��0.6{9}^{2}$=0.27451926��
P��X=3��=${C}_{4}^{3}��0.3{1}^{3}��0.69$=0.08222316��
P��X=4��=${C}_{4}^{4}��0.3{1}^{4}$=0.00923521��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.22667121 | 0.40735116 | 0.27451926 | 0.08222316 | 0.00923521 |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ�����ʵ�Ӧ�ã�������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע�����ֲ������ʵĺ������ã�


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
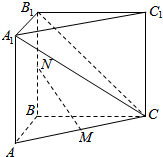 ��ͼ��������ABC-A1B1C1�У�AB=BC=2��AC=2$\sqrt{2}$������ABB1A1�Ǿ��Σ�M��N�ֱ���AC��BB1���е㣮
��ͼ��������ABC-A1B1C1�У�AB=BC=2��AC=2$\sqrt{2}$������ABB1A1�Ǿ��Σ�M��N�ֱ���AC��BB1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-1���ȣ�0��+�ޣ� | B�� | ��-�ޣ�-1���ȣ�0��1���ȣ�1��+�ޣ� | C�� | ��-1��0���ȣ�1��+�ޣ� | D�� | ��-1��0���ȣ�0��1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com