
分析 根据函数奇偶性的定义进行判断即可.
解答 解:(1)要使函数有意义,则$\left\{\begin{array}{l}{1+x≥0}\\{1-x≠0}\end{array}\right.$,即$\left\{\begin{array}{l}{x≥-1}\\{x≠1}\end{array}\right.$,即x≥-1且x≠1,函数的定义域关于原点不对称,故f(x)=$\frac{(x-1)\sqrt{1+x}}{1-x}$为非奇非偶函数;
(2)由$\left\{\begin{array}{l}{x^2-1≥0}\\{1-x^2≥0}\end{array}\right.$,则$\left\{\begin{array}{l}{x^2≥1}\\{x^2≤1}\end{array}\right.$,即x2=1,
即x=1或x=-1,即函数的定义域为{1,-1},
此时f(x)=$\sqrt{{x}^{2}-1}$+$\sqrt{1-{x}^{2}}$=0,则f(x)既是奇函数也是偶函数.
(3)∵f(-x)=3|-x|=3|x|=f(x),
∴f(x)为偶函数.
(4)由x2-3≠0得x≠±$\sqrt{3}$,即定义域为{$\sqrt{3}$,-$\sqrt{3}$},
∵f(-x)=$\frac{-3x}{{x}^{2}-3}$=-$\frac{3x}{{x}^{2}-3}$=-f(x).
∴f(x)为奇函数.
点评 本题主要考查函数奇偶性的判断,注意要先判断定义域是否关于原点对称.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3.4,0) | B. | (13,0) | C. | (5,0) | D. | (1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
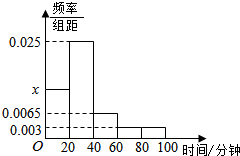 古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].
古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com