
分析 (1)由题意知现从甲袋中有放回的摸出一球,每次摸到白球的概率都是$\frac{2}{3}$,从乙袋中有放回的摸出一球,每次摸到白球的概率都是$\frac{3}{4}$,由此利用n次独立重复试验中事件A恰到好发生k次的概率计算公式能求出从甲袋中恰有一次摸出白球同时在乙袋中恰有一次摸出红球的概率.
(2)从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的情况有:从甲袋中摸出2次白球,从乙袋摸出0次白球;从甲袋中摸出1次白球,从乙袋摸出1次白球;从甲袋中摸出0次白球,从乙袋摸出2次白球,由此能求出从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的概率.
(3)由题意得从甲袋中摸出白球的次数ξ~B(3,$\frac{2}{3}$),由此能求出Eξ.
解答 解:(1)由题意知现从甲袋中有放回的摸出一球,每次摸到白球的概率都是$\frac{2}{3}$,
从乙袋中有放回的摸出一球,每次摸到白球的概率都是$\frac{3}{4}$,
∴从甲袋中连续3次有放回的摸出一球,从乙袋中连续2次有放回的摸出一球.
从甲袋中恰有一次摸出白球同时在乙袋中恰有一次摸出红球的概率:
p1=${C}_{3}^{1}(\frac{2}{3})(\frac{1}{3})^{2}$+${C}_{2}^{1}(\frac{3}{4})(\frac{1}{4})$=$\frac{43}{72}$.
(2)从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的情况有:
从甲袋中摸出2次白球,从乙袋摸出0次白球;从甲袋中摸出1次白球,从乙袋摸出1次白球;从甲袋中摸出0次白球,从乙袋摸出2次白球,
∴从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的概率:
p2=${C}_{3}^{2}(\frac{2}{3})^{2}(\frac{1}{3}){C}_{2}^{0}(\frac{1}{4})^{2}$+${C}_{3}^{1}(\frac{2}{3})(\frac{1}{3})^{2}{C}_{2}^{1}(\frac{3}{4})(\frac{1}{4})$+${C}_{3}^{0}(\frac{1}{3})^{3}{C}_{2}^{2}(\frac{3}{4})^{2}$
=$\frac{25}{144}$.
(3)由题意得从甲袋中摸出白球的次数ξ~B(3,$\frac{2}{3}$),
∴Eξ=3×$\frac{2}{3}=2$.
点评 本题考查概率的求法,考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰到好发生k次的概率计算公式和二项分布的数学期望计算公式的合理运用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
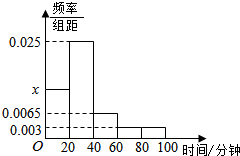 古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].
古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com