
| A�� | $[{2k��+\frac{��}{6}\;��\;2k��+\frac{��}{3}}]$ | B�� | $[{2k��+\frac{��}{6}\;��\;2k��+\frac{��}{2}}]$ | C�� | $[{2k��+\frac{��}{3}\;��\;2k��+\frac{��}{2}}]$ | D�� | $[{2k��-\frac{7��}{6}��2k��-\frac{��}{6}}]$ |
���� ��������ĵ������õ������ĵ������䣬�ⲻ��ʽ�鼴�ɣ�
��� �⣺��f��x��=x+2cosx��
��f�䣨x��=1-2sinx��
��f�䣨x��=1-2sinx��0����sinx��$\frac{1}{2}$��
��x��[2k��-$\frac{7��}{6}$��2k��+$\frac{��}{6}$]��
��f��x��������[t��t+$\frac{��}{3}$]�ϵ���������
��$\left\{\begin{array}{l}{t��2k��-\frac{7��}{6}}\\{t+\frac{��}{3}��2k��+\frac{��}{6}}\end{array}\right.$��
��ã�t��[2k��-$\frac{7��}{6}$��2k��-$\frac{��}{6}$]��
��ѡ��D��
���� ���⿼���˺����ĵ��������⣬���鵼����Ӧ���Լ����Ǻ������⣬��һ�������⣮


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+y2=1 | B�� | x2-y+3=0 | C�� | $y=\sqrt{x-3}+\sqrt{2-x}+3$ | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�����ABCD��ֱ�����Σ�AD��BC��AB��BC������PAB�͵���ABCD��PA=AD=AB=1��BC=2��
��ͼ��������P-ABCD�У�����ABCD��ֱ�����Σ�AD��BC��AB��BC������PAB�͵���ABCD��PA=AD=AB=1��BC=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
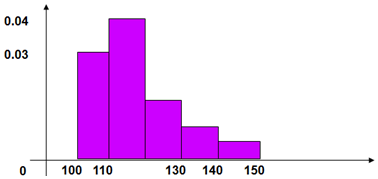
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{2}{5}$ | C�� | -$\frac{2}{5}$ | D�� | $-\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com