
分析 首先将条件转化为对任意的x∈(0,+∞),不等式[(x+lnx)-(a+lna)](-2x2+ax+10)≤0恒成立,构造函数f(x)=x+lnx,g(x)=-2x2+ax+10,由于f(x)在(0,+∞)上单调递增,故0<x<a时,(x+lnx)-(a+lna)<0,则-2x2+ax+10≥0;x>a时,(x+lnx)-(a+lna)>0恒成立,则-2x2+ax+10≤0.再根据二次函数图象及性质,即可求出a的范围.
解答 解:∵对任意的x∈(0,+∞),不等式(x-a+ln$\frac{x}{a}$)(-2x2+ax+10)≤0恒成立,
∴对任意的x∈(0,+∞),不等式[(x+lnx)-(a+lna)](-2x2+ax+10)≤0恒成立,
记f(x)=x+lnx,g(x)=-2x2+ax+10,则f(x)在(0,+∞)上单调递增
①当0<x<a时,f(x)<f(a),即(x+lnx)-(a+lna)<0恒成立,则-2x2+ax+10≥0
∴$\left\{\begin{array}{l}{g(0)=10≥0}\\{g(a)=-{a}^{2}+10≥0}\end{array}\right.$,得0<a≤$\sqrt{10}$;
②当x=a时,不等式显然恒成立;
③当x>a时,f(x)>f(a),即(x+lnx)-(a+lna)>0恒成立,则-2x2+ax+10≤0,
∵g(x)=-2(x-$\frac{a}{4}$)2+$\frac{{a}^{2}}{8}$+10在(a,+∞)上单调递减,
∴x>a时,g(x)<g(a)=10-a2≤0,得a≤$\sqrt{10}$.
综上可得,a=$\sqrt{10}$.
点评 本题考查了恒成立问题,转化思想和分类讨论是解决问题的关键,综合性较强.


科目:高中数学 来源: 题型:解答题
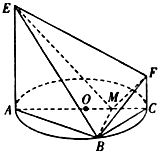 如图,AC是圆O的直径,点 B在圆 O上,∠B AC=30°,B M⊥AC交 AC于点 M,E A⊥平面 A BC,FC∥E A,AC=4,E A=3,FC=1.
如图,AC是圆O的直径,点 B在圆 O上,∠B AC=30°,B M⊥AC交 AC于点 M,E A⊥平面 A BC,FC∥E A,AC=4,E A=3,FC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{36}$] | B. | (0,$\frac{1}{9}$] | C. | (0,$\frac{1}{6}$] | D. | (0,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 240 | C. | 500 | D. | 512 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 导函数为$f'(x)=3cos(2x-\frac{π}{3})$ | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{2}$对称 | |
| C. | 函数f(x)在区间$(-\frac{π}{12},\frac{5π}{12})$上是增函数 | |
| D. | 函数f(x)的图象可由函数y=3sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{2kπ+\frac{π}{6}\;,\;2kπ+\frac{π}{3}}]$ | B. | $[{2kπ+\frac{π}{6}\;,\;2kπ+\frac{π}{2}}]$ | C. | $[{2kπ+\frac{π}{3}\;,\;2kπ+\frac{π}{2}}]$ | D. | $[{2kπ-\frac{7π}{6},2kπ-\frac{π}{6}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com