解:(1)∵f'(x)=1-

,∴f'(1)=1-a
∴曲线y=f(x)在x=1处的切线的斜率为1-a
∵曲线y=f(x)在x=1处的切线的方程为3x-y-3=0,
∴1-a=3,解得a=-2
(2)①充分性
当a=1时,f(x)=x-1-lnx,f'(x)=1-

=

∴当x>1时,f'(x)>0,所以函数f(x)在(1,+∞)上是增函数,
当0<x<1时,f'(x)<0,所以函数f(x)在(0,1)上是减函数,
∴f(x)≥f(1)=0
②必要性
f'(x)=1-

=
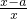
,其中x>0
(i)当a≤0时,f'(x)>0恒成立,所以函数f(x)在(0,+∞)上是增函数
而f(1)=0,所以当x∈(0,1)时,f(x)<0,与f(x)≥0恒成立相矛盾
∴a≤0不满足题意.
(ii)当a>0时,∵x>a时,f'(x)>0,所以函数f(x)在(a,+∞)上是增函数;
0<x<a时,f'(x)<0,所以函数f(x)在(0,a)上是减函数;
∴f(x)≥f(a)=a-a-alna
∵f(1)=0,所以当a≠1时,f(a)<f(1)=0,此时与f(x)≥0恒成立相矛盾
∴a=1
综上所述,f(x)≥0恒成立的充要条件是a=1;
(3)由(2)可知,
当a<0时,函数f(x)在(0,1]上是增函数,又函数y=

在(0,1]上是减函数
不妨设0<x
1≤x
2≤1
则|f(x
1)-f(x
2)|=f(x
2)-f(x
1),
∴|f(x
1)-f(x
2)|≤4|

-

|即f(x
2)+4×

≤f(x
1)+4×

设h(x)=f(x)+

=x-1-alnx+

,
则|f(x
1)-f(x
2)|≤4|

-

|等价于函数h(x)在区间(0,1]上是减函数
因为h'(x)=1-

-

=
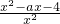
,所以x
2-ax-4≤0在(0,1]上恒成立,
即a≥x-

在(0,1]上恒成立,即a不小于y=x-

在(0,1]内的最大值.
而函数y=x-

在(0,1]是增函数,所以y=x-

的最大值为-3
所以a≥-3,又a<0,所以a∈[-3,0).
分析:(1)根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,建立等式关系即可求出a的值;
(2)先证充分性,当a=1时,利用导数研究函数的最小值即可,然后证明必要性,讨论a的符号使f(x)≥0恒成立,求出a的值即可;
(3)设h(x)=f(x)+

=x-1-alnx+

,则|f(x
1)-f(x
2)|≤4|

-

|等价于函数h(x)在区间(0,1]上是减函数即使x
2-ax-4≤0在(0,1]上恒成立,然后利用分离法将a分离出来,从而求出a的范围.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及充要条件的证明和恒成立问题的应用,同时考查了计算能力,转化与划归的思想,属于中档题.

 -
- |,求实数a的取值范围.
|,求实数a的取值范围. ,∴f'(1)=1-a
,∴f'(1)=1-a =
=
 =
=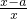 ,其中x>0
,其中x>0 在(0,1]上是减函数
在(0,1]上是减函数 -
- |即f(x2)+4×
|即f(x2)+4× ≤f(x1)+4×
≤f(x1)+4×
 =x-1-alnx+
=x-1-alnx+ ,
, -
- |等价于函数h(x)在区间(0,1]上是减函数
|等价于函数h(x)在区间(0,1]上是减函数 -
- =
=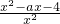 ,所以x2-ax-4≤0在(0,1]上恒成立,
,所以x2-ax-4≤0在(0,1]上恒成立, 在(0,1]上恒成立,即a不小于y=x-
在(0,1]上恒成立,即a不小于y=x- 在(0,1]内的最大值.
在(0,1]内的最大值. 在(0,1]是增函数,所以y=x-
在(0,1]是增函数,所以y=x- 的最大值为-3
的最大值为-3 =x-1-alnx+
=x-1-alnx+ ,则|f(x1)-f(x2)|≤4|
,则|f(x1)-f(x2)|≤4| -
- |等价于函数h(x)在区间(0,1]上是减函数即使x2-ax-4≤0在(0,1]上恒成立,然后利用分离法将a分离出来,从而求出a的范围.
|等价于函数h(x)在区间(0,1]上是减函数即使x2-ax-4≤0在(0,1]上恒成立,然后利用分离法将a分离出来,从而求出a的范围.

 智能训练练测考系列答案
智能训练练测考系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<