
分析 (1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,代入曲线C的极坐标方程可得直角坐标方程;由直线的参数方程的标准形式可得所求方程;
(2)将直线的参数方程代入曲线C的直角坐标方程,可得t的二次方程,运用韦达定理和参数的几何意义,即可得到所求之积.
解答 解:(1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,可得
曲线C的极坐标方程ρ2+4ρcosθ-2ρsinθ+1=0,
即为直角坐标方程x2+y2+4x-2y+1=0,
由直线l过点P(-1,1),且倾斜角为$\frac{5π}{6}$,
可得直线l的参数方程为$\left\{\begin{array}{l}{x=-1+tcos\frac{5π}{6}}\\{y=1+tsin\frac{5π}{6}}\end{array}\right.$(t为参数),
即为$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$(t为参数);
(2)直线l与曲线C交于A,B两点,
可将直线l的参数方程$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$代入曲线C的方程x2+y2+4x-2y+1=0,
可得t2-$\sqrt{3}$t-3=0,即有t1+t2=$\sqrt{3}$,t1t2=-3,
由参数t的几何意义,可得|PA|•|PB|=|t1|•|t2|
=|t1t2|=3.
点评 本题主要考查参数方程的运用,注意运用方程联立和韦达定理,考查极坐标方程和直角坐标方程的互化,考查运算能力,属于基础题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
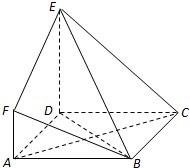 如图,四边形ABCD是菱形,DE⊥平面ABCD,AF∥DE,DE=3AF.
如图,四边形ABCD是菱形,DE⊥平面ABCD,AF∥DE,DE=3AF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
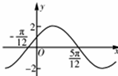 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,将函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则关于函数g(x):
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,将函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则关于函数g(x):| A. | ①③ | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline z$=$\frac{1}{2}$-$\frac{1}{2}$i | B. | $\overline z$=-$\frac{1}{2}$-$\frac{1}{2}$i | C. | $\overline z$=-1-i | D. | $\overline z$=1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∪(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
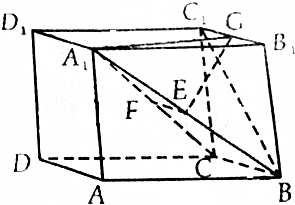 如图,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长均为a,∠ABC=60°,E、F、G分别是A1B、A1C、B1C1的中点.
如图,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长均为a,∠ABC=60°,E、F、G分别是A1B、A1C、B1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com