
分析 (1)利用列举法确定基本事件的公式,即可求出抽到的三张卡片上的数字之和大于7的概率;
(2)确定基本事件的个数,即可求两次抽取中至少有一次抽到写有数字3的卡片的概率.
解答 解:(1)设A表示事件“抽取三张卡片上的数字之和大于7”,取三张卡片,三张卡片上的数字全部可能的结果是(1,2,3),(1,2,4),(1,3,4),(2,3,4).其中数字之和大于7的是(1,3,4),(2,3,4),所以$P(A)=\frac{1}{2}$.
(2)设B表示事件“至少一次抽到写有数字3的卡片”,第一次抽1张,放回后再抽取一张卡片的基本结果有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个基本结果.
事件B包含的基本事件有(1,3),(2,3),(3,1),(3,2),(3,3),(3,4),(4,3),共7个基本结果.
所以所求事件的概率$P(B)=\frac{7}{16}$.
点评 本题考查古典概型概率的计算,考查列举法的运用,考查学生的计算能力,确定基本事件的个数是关键.


科目:高中数学 来源: 题型:选择题
| A. | 无解 | B. | 恰有一解 | C. | 恰有两个解 | D. | 有无穷多个解 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在公务员招聘中,既有笔试又有面试,某单位在2015年公务员考试中随机抽取100名考生的笔试成绩,按成绩分为5组[50,60),[60,70),[70,80),[80,90),[90,100],得到的频率分布直方图如图所示.
在公务员招聘中,既有笔试又有面试,某单位在2015年公务员考试中随机抽取100名考生的笔试成绩,按成绩分为5组[50,60),[60,70),[70,80),[80,90),[90,100],得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
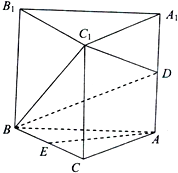 如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点.
如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | b<c<a | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
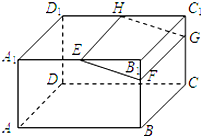 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的动点(点E与B1不重合),且EH∥A1D1,过EH的动平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,B1E+B1F=2a.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的动点(点E与B1不重合),且EH∥A1D1,过EH的动平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,B1E+B1F=2a.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率的最小值为( )| A. | $\frac{11}{12}$ | B. | $\frac{3}{4}$ | C. | $\frac{13}{16}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com