练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

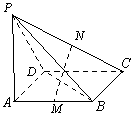
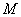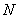    如图，，分别是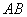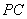，的中点。求证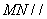：平面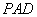；（要求用线面平行的判定定理与面面平行的性质定理两种方法证明）


    解析：（1）设PD的中点为E，连AE, NE，

    则易得四边形AMNE是平行四边形，则 MN∥AE ，

    ， 所以  MN∥平面PAD   

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014-2015学年福建省高一下学期第一次月考数学试卷（解析版） 题型：选择题

    总体由编号为01，02， ，19，20的20个个体组成，利用下面的随机数表选取6个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第6个个体的编号为（ ）

    7816

    6572

    0802

    6314

    0702

    4369

    1128

    0598

    3204

    9234

    4935

    8200

    3623

    4869

    6938

    7481

    A．11 B．02 C．05 D．04

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    棱锥的结构特征

    名称

    棱锥

    正棱锥

    图形

    特征

    ①有一个面是 (　　　　　　　　　），

    ②其余各面是有一个（　　　）的三角形．

    底面是　（　　　），并且各侧面都是全等的（　　）的棱锥．

    面积

    棱锥侧面积（　　　　　　　）

    棱锥表面积

    体积

    锥体的体积

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个几何体的三视图如图所示，则该几何体可以是（　　）

    A．棱柱      B．棱台    

    C．圆柱      D．圆台

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图所示，则该几何的体积为（    ）

    A．   　　B．  

    C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱柱ABC ­A1B1C1中，E，F分别是A1C1，BC的中点．

    图1­5

    求证：C1F∥平面ABE；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，三棱柱ABC­A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.

    (1)证明：AB⊥A1C；

    (2)若AB＝CB＝2，A1C＝，求三棱柱ABC­A1B1C1的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图，四边形为矩形，平面，，为上的点，且平面.

    (1)求证：；

    (2)设在线段上，且满足，试

    在线段上确定一点，使得∥平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为应对金融危机，刺激消费，某市给市民发放面额为100元的旅游消费卷，由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表：

    200元

    300元

    400元

    500元

    老年

    0．4

    0．3

    0．2

    0．1

    中年

    0．3

    0．4

    0．2

    0．1

    青年

    0．3

    0．3

    0．2

    0．2

    某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点，（1）求这三人恰有两人消费额不少于300元的概率；（2）求这三人消费总额大于或等于1300元的概率。

    查看答案和解析>>

    同步练习册答案