
【题目】将一张纸沿直线l对折一次后,点A(0,4)与点B(8,0)重叠,点C(6,8)与点D(m,n)重叠.
(1)求直线l的方程;
(2)求m+n的值;
(3)直线l上是否存在一点P,使得||PB|﹣|PC||存在最大值,如果存在,请求出最大值,以及此时点P的坐标;如果不存在,请说明理由.
【答案】
(1)解:设线段AB的中点为N,则点N(4,2),且 ![]()
则直线l的方程为2x﹣y﹣6=0
(2)解:设直线CD的方程为x+2y+C'=0
∵C(6,8)在直线CD上,∴C'=﹣22,则直线CD的方程为x+2y﹣22=0
设直线CD与直线l的交点为M, ![]()
![]()
则 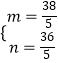 ,∴
,∴ ![]()
(3)解:假设直线l上存在点P,
∵||PB|﹣|PC||=||PA|﹣|PC||≥|AC|
当且仅当P,A,C三点共线时,等号成立
直线AC的方程为x﹣3y+12=0
∴ ![]() ,∴P(6,6)
,∴P(6,6)
【解析】(1)设线段AB的中点为N,则点N(4,2),且 ![]() ,即可求出直线l的方程;(2)求出直线CD的方程,可得直线CD与直线l的交点坐标,即可求m+n的值;(3)假设直线l上存在点P,利用||PB|﹣|PC||=||PA|﹣|PC||≥|AC|,得出结论.
,即可求出直线l的方程;(2)求出直线CD的方程,可得直线CD与直线l的交点坐标,即可求m+n的值;(3)假设直线l上存在点P,利用||PB|﹣|PC||=||PA|﹣|PC||≥|AC|,得出结论.


科目:高中数学 来源: 题型:
【题目】我们把b除a的余数r记为r=abmodb,例如4=9bmod5,如图所示,若输入a=209,b=77,则循环体“r←abmodb”被执行了次. 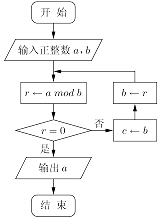
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若Ai(i=1,2,3,…,n)是△AOB所在平面内的点,且 ![]()
![]() =
= ![]()
![]() ,给出下列说法:
,给出下列说法:
·(1)| ![]() |=|
|=| ![]() |=|
|=| ![]() |=…=|
|=…=| ![]() |
|
·(2)| ![]() |的最小值一定是|
|的最小值一定是| ![]() |
|
·(3)点A和点Ai一定共线
·(4)向量 ![]() 及
及 ![]() 在向量
在向量 ![]() 方向上的投影必定相等
方向上的投影必定相等
其中正确的个数是( )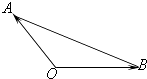
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式x2﹣ax+b<0的解集为(1,2),则不等式 ![]() <
< ![]() 的解集为( )
的解集为( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
C.( ![]() ,+∞)
,+∞)
D.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com