
分析 (1)结合规律$\frac{1}{k}$,$\frac{2}{k-1}$,$\frac{3}{k-2}$,…,$\frac{k}{1}$得:第3个值等于1的项an=$\frac{3}{3}$,进而求出n的值;
(2)将数列分组:$\frac{1}{1}$,($\frac{1}{2}$,$\frac{2}{1}$),($\frac{1}{3}$,$\frac{2}{2}$,$\frac{3}{1}$),…,($\frac{1}{k}$,$\frac{2}{k-1}$,$\frac{3}{k-2}$,…,)$\frac{k}{1}$,…,根据数列的规律和等差数列的前n项和公式求出第2015项的值.
解答 解:(1)若an是第3个值等于1的项,则an=$\frac{3}{3}$,求得n=1+2+3+4+3=13;
故答案是:13;
(2):(1)将数列分组:$\frac{1}{1}$,($\frac{1}{2}$,$\frac{2}{1}$),($\frac{1}{3}$,$\frac{2}{2}$,$\frac{3}{1}$),…,($\frac{1}{k}$,$\frac{2}{k-1}$,$\frac{3}{k-2}$,…)$\frac{k}{1}$,…,
因为1+2+3+…+62=1953,1+2+3+…+63=2016,
所以数列的第2015项属于第63组倒数第1个数,即为$\frac{62}{2}$=31;
故答案是:31.
点评 本题考查了规律型:数字的变化,有一定的难度,找到分子分母的和与分数的个数的关系,以及分子分母的和为偶数的项中,有一个值等于1的规律是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10种 | B. | 20种 | C. | 30种 | D. | 40种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3] | B. | [-1,3] | C. | (-∞,-1)∪[3,+∞) | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?
如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
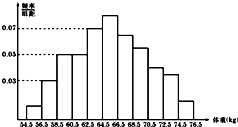 为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.
为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com