
一企业生产的某产品在不做电视广告的前提下,每天销售量为b吨.经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量S(吨)与电视广告每天的播放量n(次)的关系可用如图所示的程序框图来体现.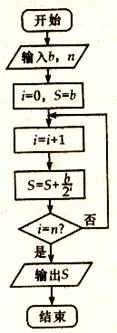
(1)试写出该产品每天的销售量S(吨)关于电视广告每天的播放量n(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加90%,则每天电视广告的播放量至少需多少次?
(1)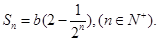 ;
;
(2)至少需4次
解析试题分析:(1)设电视广告播放量为每天i次时,该产品的销售量为si(0≤i≤n,)根据循环体可得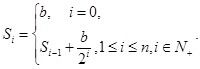 再用数列中的累加法求得sn;
再用数列中的累加法求得sn;
(2)“要使该产品每天的销售量比不做电视广告时的销售量至少增加90%”根据(1)则有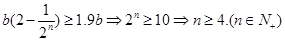 ,或通过验证得到结果.
,或通过验证得到结果.
试题解析:(1)解:设电视广告播放量为每天i次时,该产品的销售量为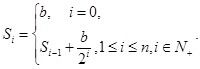 于是当
于是当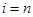 时,
时,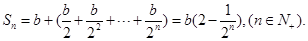 5分
5分
所以,该产品每天销售量S(吨)与电视广告播放量n(次/天)的函数关系式为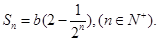 7分
7分
(2)由题意,有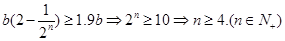 所以,要使该产品的销售量比不做电视广告时的销售量增加90%,则每天广告的播放量至少需4次. 12分
所以,要使该产品的销售量比不做电视广告时的销售量增加90%,则每天广告的播放量至少需4次. 12分
考点:1.考查函数模型的建立和应用;2.程序框图;3.累加法和指数不等式的解法


科目:高中数学 来源: 题型:解答题
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一般情况下,大桥上的车流速度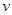 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到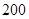 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当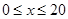 时,车流速度为
时,车流速度为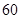 千米/小时.研究表明:当
千米/小时.研究表明:当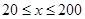 时,车流速度
时,车流速度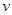 是车流密度
是车流密度 的一次函数.
的一次函数.
(1)当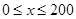 时,求函数
时,求函数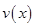 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)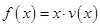 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数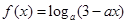 .
.
(1) 当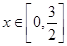 时,函数
时,函数 恒有意义,求实数a的取值范围;
恒有意义,求实数a的取值范围;
(2) 是否存在这样的实数a,使得函数 在区间
在区间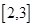 上为增函数,并且
上为增函数,并且 的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.
的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
工厂生产某种产品,次品率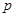 与日产量
与日产量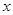 (万件)间的关系
(万件)间的关系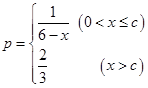 (
( 为常数,且
为常数,且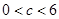 ),已知每生产一件合格产品盈利
),已知每生产一件合格产品盈利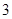 元,每出现一件次品亏损
元,每出现一件次品亏损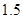 元.
元.
(1)将日盈利额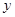 (万元)表示为日产量
(万元)表示为日产量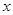 (万件)的函数;
(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注:  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一家公司生产某种产品的年固定成本为10万元,每生产1千件该产品需另投入2.7万元,设该公司一年内生产该产品 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为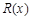 万元,且
万元,且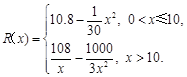
(Ⅰ)写出年利润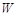 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一产品的产销过程中所获利润最大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com