
在一般情况下,大桥上的车流速度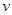 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到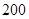 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当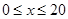 时,车流速度为
时,车流速度为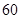 千米/小时.研究表明:当
千米/小时.研究表明:当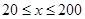 时,车流速度
时,车流速度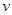 是车流密度
是车流密度 的一次函数.
的一次函数.
(1)当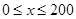 时,求函数
时,求函数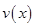 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)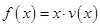 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
(1)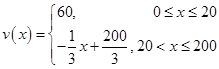 ;
;
(2)当车流密度为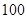 辆/千米时,车流量达到最大,且最大值约
辆/千米时,车流量达到最大,且最大值约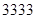 辆/小时.
辆/小时.
解析试题分析:(1)先根据题中函数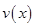 在区间
在区间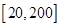 上为一次函数,设
上为一次函数,设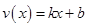 ,利用
,利用 和
和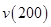 的值列方程组解出
的值列方程组解出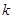 和
和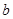 的值,从而确定函数
的值,从而确定函数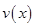 的解析式;(2)利用(1)中函数
的解析式;(2)利用(1)中函数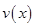 的解析式,将函数
的解析式,将函数 的解析式确定下来(分段函数),然后分别求出函数
的解析式确定下来(分段函数),然后分别求出函数 在区间
在区间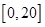 与
与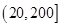 上的最大值,并比较大小,从而确定函数
上的最大值,并比较大小,从而确定函数 在定义域
在定义域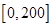 的最大值,进而确定相应的车流密度与车流量.
的最大值,进而确定相应的车流密度与车流量.
试题解析:(1)当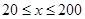 时,设
时,设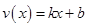 ,
,
则有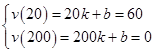 ,解得
,解得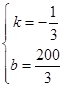 ,
,
所以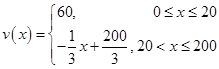 ;
;
(2)由题意知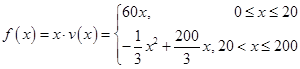 ,
,
当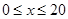 时,
时,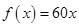 ,则函数
,则函数 在区间
在区间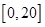 上单调递增,此时
上单调递增,此时 在
在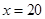 处取最大值,
处取最大值,
即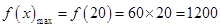 ;
;
当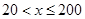 时,
时,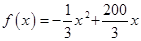 ,函数图象开口朝上,对称轴为直线
,函数图象开口朝上,对称轴为直线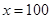 ,
,
此时函数 在
在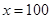 处取得最大值,即
处取得最大值,即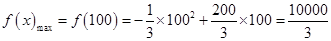 ,
,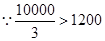 ,故当
,故当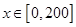 时,
时,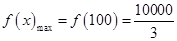 ,
,
即当车流密度为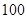 辆/千米时,车流量达到最大,且最大值约
辆/千米时,车流量达到最大,且最大值约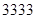 辆/小时.
辆/小时.
考点:1.函数解析式;2.分段函数的最值


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
一企业生产的某产品在不做电视广告的前提下,每天销售量为b吨.经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量S(吨)与电视广告每天的播放量n(次)的关系可用如图所示的程序框图来体现.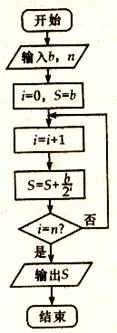
(1)试写出该产品每天的销售量S(吨)关于电视广告每天的播放量n(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加90%,则每天电视广告的播放量至少需多少次?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某社区有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动 小时的收费为
小时的收费为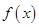 元
元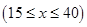 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动 小时的收费为
小时的收费为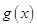 元
元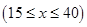 .试求
.试求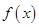 和
和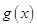 .
.
(2)问:小张选择哪家比较合算?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com