
已知函数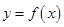 和
和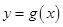 的图象关于
的图象关于 轴对称,且
轴对称,且 .
.
(1)求函数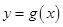 的解析式;
的解析式;
(2)当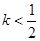 时,解不等式
时,解不等式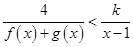 .
.
(1)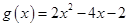 ;(2)当
;(2)当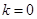 ,解集为
,解集为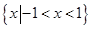 ;
;
当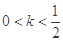 ,解集为
,解集为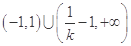 ;当
;当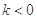 ,解集为
,解集为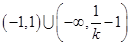 .
.
解析试题分析:(1)先利用两个函数图象关于 轴对称的关系,得出函数
轴对称的关系,得出函数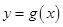 上的点
上的点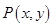 与其关于
与其关于 轴对称点
轴对称点 在函数
在函数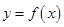 ,进而通过坐标之间的关系得出函数
,进而通过坐标之间的关系得出函数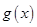 的解析式;(2)先将不的公式进行等价变形,得到
的解析式;(2)先将不的公式进行等价变形,得到 ,等价转化为
,等价转化为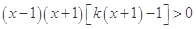 ,就
,就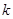 的取值进行分类讨论,主要是对
的取值进行分类讨论,主要是对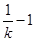 与
与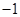 和
和 的大小进行分类讨论,从而确定不等式的解集.
的大小进行分类讨论,从而确定不等式的解集.
试题解析:(1)设函数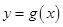 图象上任意一点
图象上任意一点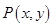 ,
,
由已知点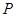 关于
关于 轴对称点
轴对称点 一定在函数
一定在函数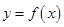 图象上,
图象上,
代入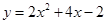 ,得
,得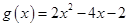 ;
;
(2)由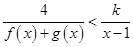 整理得不等式为
整理得不等式为 ,
,
等价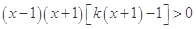 ,
,
当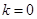 ,不等式为
,不等式为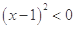 ,解为
,解为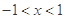 .
.
当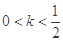 ,整理为
,整理为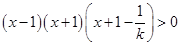 ,解为
,解为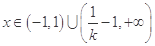 .
.
当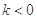 ,不等式整理为
,不等式整理为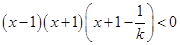 ,解为
,解为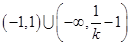 .
.
综上所述,当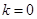 ,解集为
,解集为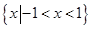 ;
;
当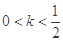 ,解集为
,解集为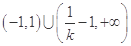 ;
;
当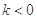 ,解集为
,解集为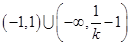 .
.
考点:1.函数图象的对称性;2.利用分类讨论法求解含参不等式


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某商品在近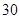 天内每件的销售价格
天内每件的销售价格 (元)与时间
(元)与时间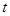 (天)的函数关系是
(天)的函数关系是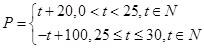 该商品的日销售量
该商品的日销售量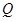 (件)与时间
(件)与时间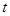 (天)的函数关系是
(天)的函数关系是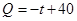
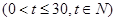 ,设商品的日销售额为
,设商品的日销售额为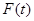 (销售量与价格之积)
(销售量与价格之积)
(1)求商品的日销售额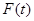 的解析式;
的解析式;
(2)求商品的日销售额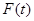 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知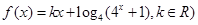 是偶函数.
是偶函数.
(1)求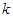 的值;
的值;
(2)证明:对任意实数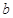 ,函数
,函数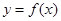 的图像与直线
的图像与直线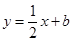 最多只有一个交点;
最多只有一个交点;
(3)设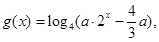 若函数
若函数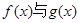 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一般情况下,大桥上的车流速度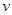 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到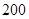 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当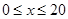 时,车流速度为
时,车流速度为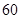 千米/小时.研究表明:当
千米/小时.研究表明:当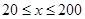 时,车流速度
时,车流速度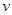 是车流密度
是车流密度 的一次函数.
的一次函数.
(1)当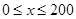 时,求函数
时,求函数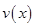 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)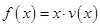 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
二次函数f(x)满足f (x+1)-f (x)=2x且f (0)=1.
⑴求f (x)的解析式;
⑵在区间[-1,1]上,y=f (x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com