设函数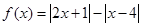
．
(I）解不等式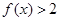
；
(II）求函数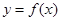
的最小值．
科目：高中数学 来源： 题型：解答题
有一块边长为4米的正方形钢板，现对其进行切割，焊接成一个长方体无盖容器（切、焊损耗忽略不计），有人用数学知识作了如下设计：在钢板的四个角处各切去一个小正方形，剩余部分围成长方体。
（Ⅰ）求这种切割、焊接而成的长方体的最大容积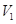
.
（Ⅱ）请问：能重新设计，使所得长方体的容器的容积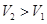
吗？若能、给出你的一种设计方案。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
运货卡车以每小时
千米的速度匀速行驶130千米
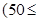
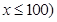（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油
升，司机的工资是每小时14元.
（1）求这次行车总费用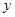
关于的表达式；
（2）当为何值时，这次行车的总费用最低，并求出最低费用的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某种汽车的购车费用是10万元，每年使用的保险费、养路费、汽油费约为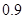
万元，年维修费用第一年是
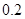万元，第二年是
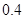万元，第三年是
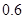万元，…，以后逐年递增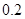万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
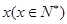年的维修费用的和为
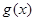，年平均费用为
.
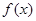(1）求出函数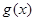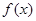，的解析式；
(2）这种汽车使用多少年时，它的年平均费用最小？最小值是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某公园准备建一个摩天轮，摩天轮的外围是一个周长为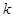
米的圆．在这个圆上安装座位，且每个座位和圆心处的支点都有一根直的钢管相连．经预算，摩天轮上的每个座位与支点相连的钢管的费用为
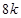元/根，且当两相邻的座位之间的圆弧长为
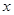米时，相邻两座位之间的钢管和其中一个座位的总费用为
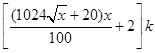元．假设座位等距离分布，且至少有两个座位，所有座位都视为点，且不考虑其他因素，记摩天轮的总造价为
元．
（Ⅰ）试写出关于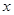的函数关系式，并写出定义域；
（Ⅱ）当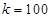
米时，试确定座位的个数，使得总造价最低？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；(Ⅱ) 
.
写成分段函数的形式，根据分段函数的解析式作出函数的图像，然后求出直线
与函数图像的交点坐标为
和
，利用数形结合的思想可知
的解集；(Ⅱ)找到函数图像的最低点，求出最低点的纵坐标即可.
，
时，函数
，
.
的解析式；
的方程
，
时，对任意
总有
成立，求
的取值范围.
是定义在
上的奇函数，当
时的解析式为
.
；
.
和
的图象关于
轴对称，且
.
时，解不等式
.