已知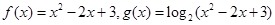
，且两函数定义域均为
，
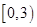（1）．画函数
在定义域内的图像，并求值域；（5分）
（2）．求函数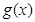
的值域．（5分）
科目：高中数学 来源： 题型：解答题
某种汽车的购车费用是10万元，每年使用的保险费、养路费、汽油费约为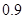
万元，年维修费用第一年是
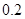万元，第二年是
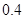万元，第三年是
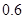万元，…，以后逐年递增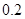万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
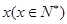年的维修费用的和为
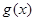，年平均费用为
.
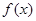(1）求出函数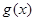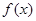，的解析式；
(2）这种汽车使用多少年时，它的年平均费用最小？最小值是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知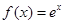
，
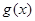为其反函数.
（Ⅰ）说明函数
与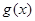图象的关系（只写出结论即可）；
（Ⅱ）证明的图象恒在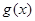的图象的上方；
（Ⅲ）设直线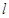
与、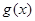均相切，切点分别为（
）、（
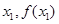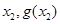），且
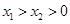，求证：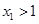
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）
；
，所以
，即
，
集合
求函数
的解析式；
,且
设
上的最大值、最小值分别为
，记
，求
的最小值.
和
的图象关于
轴对称，且
.
时，解不等式
.
．
为何实数，
总是增函数；
是关于
的方程
的两个根，且
.
与
之间满足的关系式；
，若存在
，使不等式
在其定义域范围内恒成立，求
，
.
的表达式（不需证明）；
的最大值为
，
，求
的最小值.
，
，
的定义域为
的值；
在区间
的取值范围。