
已知函数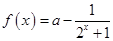 .
.
(1)求证不论 为何实数,
为何实数, 总是增函数;
总是增函数;
(2)确定 的值,使
的值,使 为奇函数;
为奇函数;
(3)当 为奇函数时,求
为奇函数时,求 的值域.
的值域.
(Ⅰ)见下(Ⅱ)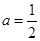 (Ⅲ)
(Ⅲ)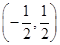
解析试题分析:(1)函数的单调性的证明有两种基本的方法.一是定义法;而是利用导数.在目前阶段,我们只能用定义来证明函数的单调性.即分三个步骤:①设值②作差③比较差值与0的关系.(2)作为奇函数,满足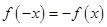 ,可求得
,可求得 的值.(Ⅲ)求函数的值域,根据函数解析式的特点,有各种不同的方法,一般有直接观察法、换元法、单调性法、判别式法、图像法等.本题中函数值域的求得较为简单,用直接观察法即可.
的值.(Ⅲ)求函数的值域,根据函数解析式的特点,有各种不同的方法,一般有直接观察法、换元法、单调性法、判别式法、图像法等.本题中函数值域的求得较为简单,用直接观察法即可.
试题解析(1)∵ 的定义域为R,任取
的定义域为R,任取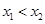
则
∵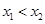 ∴
∴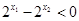 ,
,
∴ 即
即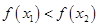
∴不论 为何实数
为何实数 总为增函数, 6分
总为增函数, 6分
(2)∵ 为奇函数,∴
为奇函数,∴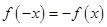
即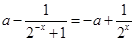 解得
解得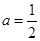 8分
8分
(3)由(2)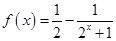
∵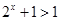 ∴
∴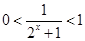 ∴
∴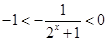
∴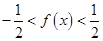
∴ 的值域为
的值域为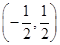 12分
12分
考点:函数的奇偶性、增减性和值域.


科目:高中数学 来源: 题型:解答题
对于函数 若存在
若存在 ,使得
,使得 成立,则称
成立,则称 为
为 的不动点.
的不动点.
已知
(1)当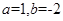 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上
图象上 、
、 两点的横坐标是函数
两点的横坐标是函数 的不动点,且
的不动点,且 、
、 两点关于直线
两点关于直线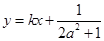 对称,求
对称,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因。暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数。当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,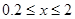 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。
(Ⅰ)当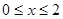 时,求函数V(x)的表达式;
时,求函数V(x)的表达式;
(Ⅱ)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时) 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为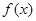 万元,且
万元,且
(1)写出年利润 (万元)关于年产品
(万元)关于年产品 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该企业生产此产品所获年利润最大?
(注:年利润=年销售收入-年总成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com