
“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因。暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数。当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,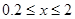 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。
(Ⅰ)当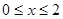 时,求函数V(x)的表达式;
时,求函数V(x)的表达式;
(Ⅱ)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时) 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。
(Ⅰ) ;(Ⅱ)当杂物垃圾密度
;(Ⅱ)当杂物垃圾密度 千克/立方米,f(x)取得最大值50千克/小时.
千克/立方米,f(x)取得最大值50千克/小时.
解析试题分析:(Ⅰ)当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时说明函数图像过 ,与
,与 ,又因为当
,又因为当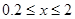 时,排水量V是垃圾杂物密度x的一次函数,可设
时,排水量V是垃圾杂物密度x的一次函数,可设 ,将
,将 与
与 代入可求出
代入可求出 ,而在
,而在 ,
, ,从而得
,从而得 的解析式;(Ⅱ)当垃圾杂物密度x为多大时,垃圾杂物量
的解析式;(Ⅱ)当垃圾杂物密度x为多大时,垃圾杂物量 可以达到最大,由
可以达到最大,由 ,这是一个分段函数,分段函数的最值分段求,然后比较谁最大为谁,当
,这是一个分段函数,分段函数的最值分段求,然后比较谁最大为谁,当 ,是一个一次函数,当
,是一个一次函数,当 时最大,最大值为
时最大,最大值为 ,当
,当 ,这是一个二次函数,对称轴为
,这是一个二次函数,对称轴为 ,故
,故 时最大,最大值为
时最大,最大值为 ,从而得当杂物垃圾密度
,从而得当杂物垃圾密度 千克/立方米,f(x)取得最大值50千克/小时.
千克/立方米,f(x)取得最大值50千克/小时.
试题解析:(Ⅰ)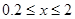 时,排水量V是垃圾杂物密度x的一次函数,设为
时,排水量V是垃圾杂物密度x的一次函数,设为 ,将
,将 与
与 代入得
代入得 ,
, (6分)
(6分)
(Ⅱ)
 千克/小时
千克/小时 ,
,
所以,当杂物垃圾密度 千克/立方米,f(x)取得最大值50千克/小时。(13分)
千克/立方米,f(x)取得最大值50千克/小时。(13分)
分)
考点:应用题,分段函数最值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
集合A是由适合以下性质的函数 构成的:对于定义域内任意两个不相等的实数
构成的:对于定义域内任意两个不相等的实数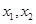 ,都有
,都有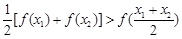 .
.
(1)试判断 =
=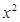 及
及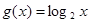 是否在集合A中,并说明理由;
是否在集合A中,并说明理由;
(2)设 ÎA且定义域为(0,+¥),值域为(0,1),
ÎA且定义域为(0,+¥),值域为(0,1), ,试写出一个满足以上条件的函数
,试写出一个满足以上条件的函数 的解析式,并给予证明.
的解析式,并给予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳a元(a为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x元时,产品一年的销售量为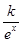 (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(Ⅰ)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,并求出L(x)的最大值.
参考公式: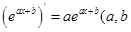 为常数
为常数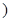 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某公司生产品牌服装的年固定成本为10万元,每生产千件,须另投入2.7万元,设该公司年内共生产品牌服装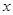 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为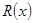 万元,且
万元,且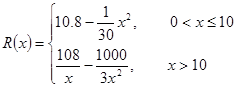 .
.
(1)写出年利润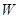 (万元)关于年产量
(万元)关于年产量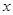 (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板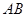 长为2m,跳水板距水面
长为2m,跳水板距水面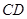 的高
的高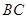 为3m,
为3m, =5m,
=5m,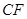 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点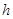 m(
m(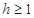 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以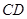 为横轴,
为横轴, 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.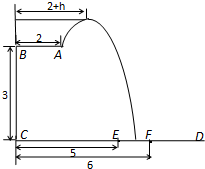
(1)当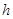 =1时,求跳水曲线所在的抛物线方程;
=1时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域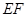 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时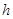 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com